题目内容
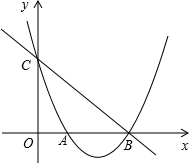 如图,在平面直角坐标系xOy中,抛物线y=x2+bx+c与y轴交于点C,与x轴交于A,B两点,点B的坐标为B(3,0),直线y=-x+3恰好经过B,C两点.
如图,在平面直角坐标系xOy中,抛物线y=x2+bx+c与y轴交于点C,与x轴交于A,B两点,点B的坐标为B(3,0),直线y=-x+3恰好经过B,C两点.(1)求抛物线y=x2+bx+c的解析式及顶点D的坐标;
(2)求抛物线的对称轴直线,并用尺规作图在对称轴直线上作出P点,使∠APD=∠ACB;
(3)在(2)的条件下求点P的坐标.
考点:二次函数综合题
专题:
分析:(1)根据直线方程易求点C、B的坐标.把它们的坐标代入二次函数解析式,利用待定系数法求得该抛物线的解析式;然后把抛物线解析式转化为顶点式方程,由顶点式方程直接写出点D的坐标;
(2)利用圆周角定理可以画出点P的位置;
(3)如图,过A作AH⊥BC于点H,连接PA,设直线x=2交x轴于E点.易证△BOC、△AHB为等腰直角三角形,则BC=3
,AH=BH=
,CH=3
-
=2
,通过解Rt△AHC中,求得PE=2.故坐标为(2,2)或(2,-2),
(2)利用圆周角定理可以画出点P的位置;
(3)如图,过A作AH⊥BC于点H,连接PA,设直线x=2交x轴于E点.易证△BOC、△AHB为等腰直角三角形,则BC=3
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
解答: 解:(1)∵y=-x+3恰好经过B,C两点,
解:(1)∵y=-x+3恰好经过B,C两点,
∴C(0,3),B(3,0),
∴
.
解之得,
.
∴抛物线的解析式为y=x2-4x+3
∵y=x2-4x+3=(x-2)2-1,
∴顶点D(2,-1);
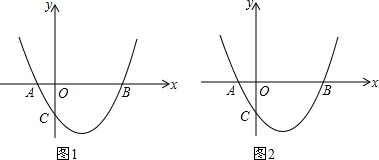
(2)如图1,点P是△ACB外接圆圆心;
(3)如图2,过A作AH⊥BC于点H,连接PA,设直线x=2交x轴于E点.
∵OB=OC=3,
∴△BOC为等腰直角三角形,∠OBC=45.,BC=3
,
又AB=2,
∴AH=BH=
,CH=3
-
=2
,
∴在Rt△AHC中,tan∠ACB=tan∠ACH=
=
,
故tan∠APE=tan∠ACB=
∵tan∠APE=
=
,
∴PE=2.
故坐标为(2,2)或(2,-2),
 解:(1)∵y=-x+3恰好经过B,C两点,
解:(1)∵y=-x+3恰好经过B,C两点,∴C(0,3),B(3,0),
∴
|
解之得,
|
∴抛物线的解析式为y=x2-4x+3
∵y=x2-4x+3=(x-2)2-1,
∴顶点D(2,-1);
(2)如图1,点P是△ACB外接圆圆心;

(3)如图2,过A作AH⊥BC于点H,连接PA,设直线x=2交x轴于E点.
∵OB=OC=3,
∴△BOC为等腰直角三角形,∠OBC=45.,BC=3
| 2 |
又AB=2,
∴AH=BH=
| 2 |
| 2 |
| 2 |
| 2 |
∴在Rt△AHC中,tan∠ACB=tan∠ACH=
| AH |
| CH |
| 1 |
| 2 |
故tan∠APE=tan∠ACB=
| 1 |
| 2 |
∵tan∠APE=
| AP |
| PE |
| 1 |
| PE |
∴PE=2.
故坐标为(2,2)或(2,-2),
点评:本题前两问考查了二次函数的基本性质,较为简单.第三问结合二次函数的图象考查了三角形的性质,综合性较强.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
下列一元二次方程中,两根之和为2的是( )
| A、x2-x+2=0 |
| B、x2+2x+2=0 |
| C、x2+x-2=0 |
| D、x2-2x=0 |
 如图,在平面直角坐标系中,直线y=-2x+42交x轴于点A,交直线y=x于点B.抛物线y=ax2-2x+c分别交线段AB、OB于点C、D,点C和点D的横坐标分别为16和4,点P在这条抛物线上.
如图,在平面直角坐标系中,直线y=-2x+42交x轴于点A,交直线y=x于点B.抛物线y=ax2-2x+c分别交线段AB、OB于点C、D,点C和点D的横坐标分别为16和4,点P在这条抛物线上. 尺规作图,如图,已知∠α,∠β(∠α>∠β),用直尺和圆规求作一个角,使得这个角等于∠α+∠β(只须作出正确图形,保留作图痕迹,不必写出作法)
尺规作图,如图,已知∠α,∠β(∠α>∠β),用直尺和圆规求作一个角,使得这个角等于∠α+∠β(只须作出正确图形,保留作图痕迹,不必写出作法) 如图,已知∠1+∠3=180°,CD⊥AD,CM平分∠DCE,求∠4的度数.
如图,已知∠1+∠3=180°,CD⊥AD,CM平分∠DCE,求∠4的度数.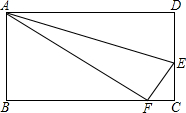 把长方形ABCD沿着AE折叠,使点D落在BC边上的点F处,已知AB=8,BC=10,
把长方形ABCD沿着AE折叠,使点D落在BC边上的点F处,已知AB=8,BC=10,