题目内容
先阅读、再解决问题.
平面直角坐标系下,一组有规律的点:
A1(0,1)、A2(1,0)、A3(2,1)、A4(3,0)、A5(4,1)、A6(5,0)…注:当n为奇数时,An(n-1,1),n为偶数时An(n-1,0).
抛物线C1经过A1,A2,A3三点,抛物线C2经过A2,A3,A4三点,抛物线C3经过A3,A4,A5三点,抛物线C4经过A4,A5,A6三点,…抛物线Cn经过An,An+1,An+2.
(1)直接写出抛物线C1,C4的解析式;
(2)若点E(e,f1)、F(e,f2)分别在抛物线C27、C28上,当e=29时,求证:△A28EF是直角三角形;
(3)若直线x=m分别交x轴、抛物线C2013、C2014于点P、M、N,作直线A2014M、A2014N,当∠PA2014M=45°时,求sin∠PA2014N的值.
平面直角坐标系下,一组有规律的点:
A1(0,1)、A2(1,0)、A3(2,1)、A4(3,0)、A5(4,1)、A6(5,0)…注:当n为奇数时,An(n-1,1),n为偶数时An(n-1,0).
抛物线C1经过A1,A2,A3三点,抛物线C2经过A2,A3,A4三点,抛物线C3经过A3,A4,A5三点,抛物线C4经过A4,A5,A6三点,…抛物线Cn经过An,An+1,An+2.
(1)直接写出抛物线C1,C4的解析式;
(2)若点E(e,f1)、F(e,f2)分别在抛物线C27、C28上,当e=29时,求证:△A28EF是直角三角形;
(3)若直线x=m分别交x轴、抛物线C2013、C2014于点P、M、N,作直线A2014M、A2014N,当∠PA2014M=45°时,求sin∠PA2014N的值.
考点:二次函数综合题
专题:
分析:(1)根据顶点式即可求出C1,C4的解析式;
(2)由特殊出发,可以发现抛物线C27、C28的解析式应该为:y27=(x-27)2,y28=-(x-28)2+1.则得到点E(29,4)、F(29,0)、A28(27,0),根据两点之间的距离公式和勾股定理即可证明△A28EF是直角三角形;
(3)分两种情况:在A2014(2013,0)点左侧;在A2014(2013,0)点右侧;根据三角函数即可得到sin∠PA2014N的值.
(2)由特殊出发,可以发现抛物线C27、C28的解析式应该为:y27=(x-27)2,y28=-(x-28)2+1.则得到点E(29,4)、F(29,0)、A28(27,0),根据两点之间的距离公式和勾股定理即可证明△A28EF是直角三角形;
(3)分两种情况:在A2014(2013,0)点左侧;在A2014(2013,0)点右侧;根据三角函数即可得到sin∠PA2014N的值.
解答:解:(1)由顶点式求出C1的解析式为:y1=(x-1)2,C4的解析式为:y4=-(x-4)2+1.
(2)由特殊出发,可以发现这组抛物线解析式的特点:
y1=(x-1)2,
y2=-(x-2)2+1,
y3=(x-3)2,
y4=-(x-4)2+1,
…
∴抛物线C27、C28的解析式应该为:y27=(x-27)2,y28=-(x-28)2+1.
如图,此时点E(e,f1)、F(e,f2)分别为点E(29,4)、F(29,0);而点A28的坐标是(27,0),

显然△A28EF是直角三角形.
(3)由(2)中发现的规律可知,抛物线C2013、C2014解析式分别为:y2013=(x-2013)2,
y2014=-(x-2014)2+1.
点A2014坐标为(2013,0).
顺便指向,由(2)的研究经验发现,可以退回简单的抛物线C3、C4的情况来研究.分以下两种情况,如图
在A2014(2013,0)点左侧,当m=2012时,M(2012,1)此时有∠PA2014M=45°,N(2012,-3),相应的sin∠PA2014N的值为
;
在A2014(2013,0)点右侧,当m=2014时,M(2014,1)此时有∠PA2014M=45°,N(2014,1),相应的sin∠PA2014N的值为
.

(2)由特殊出发,可以发现这组抛物线解析式的特点:
y1=(x-1)2,
y2=-(x-2)2+1,
y3=(x-3)2,
y4=-(x-4)2+1,
…
∴抛物线C27、C28的解析式应该为:y27=(x-27)2,y28=-(x-28)2+1.
如图,此时点E(e,f1)、F(e,f2)分别为点E(29,4)、F(29,0);而点A28的坐标是(27,0),

显然△A28EF是直角三角形.
(3)由(2)中发现的规律可知,抛物线C2013、C2014解析式分别为:y2013=(x-2013)2,
y2014=-(x-2014)2+1.
点A2014坐标为(2013,0).
顺便指向,由(2)的研究经验发现,可以退回简单的抛物线C3、C4的情况来研究.分以下两种情况,如图
在A2014(2013,0)点左侧,当m=2012时,M(2012,1)此时有∠PA2014M=45°,N(2012,-3),相应的sin∠PA2014N的值为
3
| ||
| 10 |
在A2014(2013,0)点右侧,当m=2014时,M(2014,1)此时有∠PA2014M=45°,N(2014,1),相应的sin∠PA2014N的值为
| ||
| 2 |

点评:考查了二次函数综合题,涉及的知识点有:顶点式求抛物线的解析式,两点之间的距离公式,勾股定理逆定理,分类思想的应用,三角函数的知识.综合性较强,有一定的难度.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
一组数据:x,2,3,6,8的平均数是6,则这组数据的极差是( )
| A、9 | B、7 | C、6 | D、11 |

 如图,已知平行四边形ABCD的对角线AC、BD交于点O,过点B作BP∥AC,过点C作CP∥BD,连接OP.求证:四边形ABPO是平行四边形.
如图,已知平行四边形ABCD的对角线AC、BD交于点O,过点B作BP∥AC,过点C作CP∥BD,连接OP.求证:四边形ABPO是平行四边形.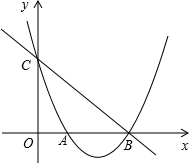 如图,在平面直角坐标系xOy中,抛物线y=x2+bx+c与y轴交于点C,与x轴交于A,B两点,点B的坐标为B(3,0),直线y=-x+3恰好经过B,C两点.
如图,在平面直角坐标系xOy中,抛物线y=x2+bx+c与y轴交于点C,与x轴交于A,B两点,点B的坐标为B(3,0),直线y=-x+3恰好经过B,C两点. 如图,在△ABC中,∠B=30°,∠BAC=105°,AB=8.求BC的长.
如图,在△ABC中,∠B=30°,∠BAC=105°,AB=8.求BC的长.