ΧβΡΩΡΎ»ί
 »γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§÷±œΏy=-2x+42ΫΜx÷α”ΎΒψAΘ§ΫΜ÷±œΏy=x”ΎΒψBΘ°≈ΉΈοœΏy=ax2-2x+cΖ÷±πΫΜœΏΕΈABΓΔOB”ΎΒψCΓΔDΘ§ΒψCΚΆΒψDΒΡΚαΉχ±ξΖ÷±πΈΣ16ΚΆ4Θ§ΒψP‘Ύ’βΧθ≈ΉΈοœΏ…œΘ°
»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§÷±œΏy=-2x+42ΫΜx÷α”ΎΒψAΘ§ΫΜ÷±œΏy=x”ΎΒψBΘ°≈ΉΈοœΏy=ax2-2x+cΖ÷±πΫΜœΏΕΈABΓΔOB”ΎΒψCΓΔDΘ§ΒψCΚΆΒψDΒΡΚαΉχ±ξΖ÷±πΈΣ16ΚΆ4Θ§ΒψP‘Ύ’βΧθ≈ΉΈοœΏ…œΘ°Θ®1Θ©«σaΓΔcΒΡ÷ΒΘ°
Θ®2Θ©»τQΈΣœΏΕΈOB…œ“ΜΒψΘ§«“PΓΔQΝΫΒψΒΡΉίΉχ±ξΕΦΈΣ5Θ§«σœΏΕΈPQΒΡ≥ΛΘ°
Θ®3Θ©»τQΈΣœΏΕΈOBΜρœΏΕΈAB…œΒΡ“ΜΒψΘ§PQΓΆx÷αΘ°…ηPΓΔQΝΫΒψ÷°ΦδΒΡΨύάκΈΣdΘ®dΘΨ0Θ©Θ§ΒψQΒΡΚαΉχ±ξΈΣmΘ§«σdΥφmΒΡ‘ω¥σΕχΦθ–Γ ±mΒΡ»Γ÷ΒΖΕΈßΘ°
Θ®4Θ©»τmin{y1Θ§y2Θ§y3}±μ Ψy1Θ§y2Θ§y3»ΐΗωΚ· ΐ÷–ΒΡΉν–Γ÷ΒΘ§‘ρΚ· ΐy=min{-2x+42Θ§xΘ§ax2-2x+c}ΒΡΉν¥σ÷ΒΈΣ
ΩΦΒψΘΚΕΰ¥ΈΚ· ΐΉέΚœΧβ
Ή®ΧβΘΚ
Ζ÷ΈωΘΚΘ®1Θ©Α―ΒψCΚΆΒψDΒΡΚαΉχ±ξ16ΚΆ4Ζ÷±π¥ζ»κΚ· ΐΩ…ΒΟCΘ®16Θ§10Θ©Θ§DΘ®4Θ§4Θ©Θ§‘ΌΗυΨί¥ΐΕ®œΒ ΐΖ®Ω…ΒΟaΓΔcΒΡ÷ΒΘΜ
Θ®2Θ©œ»«σ≥ωΒψQΒΡΉχ±ξΘ§ΒψPΒΡΉχ±ξΘ§‘ΌΖ÷ΝΫ÷÷«ιΩωΘΚΔΌΒ±ΒψP‘ΎΒψQΉσ≤ύ ±ΘΜΔΎΒ±ΒψP‘ΎΒψQ”“≤ύ ±Θ§ΗυΨίΝΫΒψ÷°ΦδΒΡΨύάκΙΪ ΫΩ…ΒΟœΏΕΈPQΒΡ≥ΛΈΣ2
-3Μρ2
+3ΘΜ
Θ®3Θ©Ιέ≤λΆΦœσΩ…÷ΣΘ§Β±0ΓήmΘΦ4Μρ14ΓήmΘΦ16 ±Θ§dΥφmΒΡ‘ω¥σΕχΦθ–ΓΘ§Β±12ΓήmΓή14 ±Θ§dΥφmΒΡ‘ω¥σΕχΦθ–ΓΘ§“ά¥ΥΦ¥Ω…«σΫβΘΜ
Θ®4Θ©’“ΒΫΝΫΗωΚ· ΐΫΜΒψΒΡΉίΉχ±ξΘ§ΒΟΒΫΤδ÷–Ήν¥σΒΡy÷ΒΦ¥ΈΣΥυ«σΘ°
Θ®2Θ©œ»«σ≥ωΒψQΒΡΉχ±ξΘ§ΒψPΒΡΉχ±ξΘ§‘ΌΖ÷ΝΫ÷÷«ιΩωΘΚΔΌΒ±ΒψP‘ΎΒψQΉσ≤ύ ±ΘΜΔΎΒ±ΒψP‘ΎΒψQ”“≤ύ ±Θ§ΗυΨίΝΫΒψ÷°ΦδΒΡΨύάκΙΪ ΫΩ…ΒΟœΏΕΈPQΒΡ≥ΛΈΣ2
| 6 |
| 6 |
Θ®3Θ©Ιέ≤λΆΦœσΩ…÷ΣΘ§Β±0ΓήmΘΦ4Μρ14ΓήmΘΦ16 ±Θ§dΥφmΒΡ‘ω¥σΕχΦθ–ΓΘ§Β±12ΓήmΓή14 ±Θ§dΥφmΒΡ‘ω¥σΕχΦθ–ΓΘ§“ά¥ΥΦ¥Ω…«σΫβΘΜ
Θ®4Θ©’“ΒΫΝΫΗωΚ· ΐΫΜΒψΒΡΉίΉχ±ξΘ§ΒΟΒΫΤδ÷–Ήν¥σΒΡy÷ΒΦ¥ΈΣΥυ«σΘ°
Ϋβ¥πΘΚ ΫβΘΚΘ®1Θ©ΓΏ‘Ύy=-2x+42÷–Θ§Β±x=16 ±Θ§y=10Θ§
ΫβΘΚΘ®1Θ©ΓΏ‘Ύy=-2x+42÷–Θ§Β±x=16 ±Θ§y=10Θ§
‘Ύy=x÷–Θ§Β±x=4 ±Θ§y=4ΘΜ
ΓύCΘ®16Θ§10Θ©Θ§DΘ®4Θ§4Θ©
ΓΏ≈ΉΈοœΏy=ax2-2x+cΨ≠ΙΐΒψCΓΔDΘ§
Γύ
Θ§
ΫβΒΟ
ΓύaΒΡ÷ΒΈΣ
Θ§cΒΡ÷ΒΈΣ10ΘΜ
Θ®2Θ©‘Ύy=x÷–Θ§Β±y=5 ±Θ§x=5Θ§
ΓύΒψQΒΡΚαΉχ±ξΈΣ5
”…Θ®1Θ©÷ΣΘ§≈ΉΈοœΏΒΡΫβΈω ΫΈΣy=
x2-2x+10Θ§
Β±y=5 ±Θ§
x2-2x+10=5Θ§ΫβΒΟx=8Γά2
ΓύΒψPΒΡΚαΉχ±ξΈΣ8Γά2
Θ°
ΔΌΒ±ΒψP‘ΎΒψQΉσ≤ύ ±Θ§œΏΕΈPQΒΡ≥ΛΈΣ5-Θ®8-2
Θ©=2
-3Θ§
ΔΎΒ±ΒψP‘ΎΒψQ”“≤ύ ±Θ§œΏΕΈPQΒΡ≥ΛΈΣΘ®8+2
Θ©-5=2
+3Θ§
ΓύœΏΕΈPQΒΡ≥ΛΈΣ2
-3Μρ2
+3ΘΜ
Θ®3Θ©Νν-2x+42=xΘ§
ΫβΒΟx=14Θ§Φ¥ΒψBΒΡΚαΉχ±ξΈΣ14
Ιέ≤λΆΦœσΩ…÷ΣΘ§Β±0ΓήmΘΦ4Μρ14ΓήmΘΦ16 ±Θ§dΥφmΒΡ‘ω¥σΕχΦθ–ΓΘ§
Β±4ΘΦmΓή14 ±Θ§d=x-Θ®
x2-2x+10Θ©=-
x2+3x-10=-
Θ®x-12Θ©2+8
”…Εΰ¥ΈΚ· ΐΆΦœσΒΡ–‘÷ Ω…÷ΣΘ§Β±12ΓήmΓή14 ±Θ§dΥφmΒΡ‘ω¥σΕχΦθ–ΓΘ§
Ήέ…œΥυ ωΘ§Β±0ΓήmΘΦ4Μρ12ΓήmΘΦ16 ±Θ§dΥφmΒΡ‘ω¥σΕχΦθ–ΓΘΜ
Θ®4Θ©ΓΏCΘ®16Θ§10Θ©Θ§
ΓύΚ· ΐy=min{-2x+42Θ§xΘ§ax2-2x+c}ΒΡΉν¥σ÷ΒΈΣ10Θ°
Ι ¥πΑΗΈΣΘΚ10Θ°
 ΫβΘΚΘ®1Θ©ΓΏ‘Ύy=-2x+42÷–Θ§Β±x=16 ±Θ§y=10Θ§
ΫβΘΚΘ®1Θ©ΓΏ‘Ύy=-2x+42÷–Θ§Β±x=16 ±Θ§y=10Θ§‘Ύy=x÷–Θ§Β±x=4 ±Θ§y=4ΘΜ
ΓύCΘ®16Θ§10Θ©Θ§DΘ®4Θ§4Θ©
ΓΏ≈ΉΈοœΏy=ax2-2x+cΨ≠ΙΐΒψCΓΔDΘ§
Γύ
|
ΫβΒΟ
|
ΓύaΒΡ÷ΒΈΣ
| 1 |
| 8 |
Θ®2Θ©‘Ύy=x÷–Θ§Β±y=5 ±Θ§x=5Θ§
ΓύΒψQΒΡΚαΉχ±ξΈΣ5
”…Θ®1Θ©÷ΣΘ§≈ΉΈοœΏΒΡΫβΈω ΫΈΣy=
| 1 |
| 8 |
Β±y=5 ±Θ§
| 1 |
| 8 |
| 6 |
ΓύΒψPΒΡΚαΉχ±ξΈΣ8Γά2
| 6 |
ΔΌΒ±ΒψP‘ΎΒψQΉσ≤ύ ±Θ§œΏΕΈPQΒΡ≥ΛΈΣ5-Θ®8-2
| 6 |
| 6 |
ΔΎΒ±ΒψP‘ΎΒψQ”“≤ύ ±Θ§œΏΕΈPQΒΡ≥ΛΈΣΘ®8+2
| 6 |
| 6 |
ΓύœΏΕΈPQΒΡ≥ΛΈΣ2
| 6 |
| 6 |
Θ®3Θ©Νν-2x+42=xΘ§
ΫβΒΟx=14Θ§Φ¥ΒψBΒΡΚαΉχ±ξΈΣ14
Ιέ≤λΆΦœσΩ…÷ΣΘ§Β±0ΓήmΘΦ4Μρ14ΓήmΘΦ16 ±Θ§dΥφmΒΡ‘ω¥σΕχΦθ–ΓΘ§
Β±4ΘΦmΓή14 ±Θ§d=x-Θ®
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 8 |
”…Εΰ¥ΈΚ· ΐΆΦœσΒΡ–‘÷ Ω…÷ΣΘ§Β±12ΓήmΓή14 ±Θ§dΥφmΒΡ‘ω¥σΕχΦθ–ΓΘ§
Ήέ…œΥυ ωΘ§Β±0ΓήmΘΦ4Μρ12ΓήmΘΦ16 ±Θ§dΥφmΒΡ‘ω¥σΕχΦθ–ΓΘΜ
Θ®4Θ©ΓΏCΘ®16Θ§10Θ©Θ§
ΓύΚ· ΐy=min{-2x+42Θ§xΘ§ax2-2x+c}ΒΡΉν¥σ÷ΒΈΣ10Θ°
Ι ¥πΑΗΈΣΘΚ10Θ°
ΒψΤάΘΚΩΦ≤ιΝΥΕΰ¥ΈΚ· ΐΉέΚœΧβΘ§…φΦΑΒΡ÷Σ ΕΒψ”–ΘΚ¥ΐΕ®œΒ ΐΖ®«σ≈ΉΈοœΏΫβΈω ΫΘ§Ζ÷άύΥΦœκΒΡ”Π”ΟΘ§ΝΫΒψ÷°ΦδΒΡΨύάκΙΪ ΫΘ§“Μ¥ΈΚ· ΐΚΆΕΰ¥ΈΚ· ΐΒΡ‘ωΦθ–‘Θ§Κ· ΐΉν÷ΒΈ ΧβΘ§ΉέΚœ–‘Ϋœ«ΩΘ§”–“ΜΕ®ΒΡΡ―Ε»Θ°

ΝΖœΑ≤αœΒΝ–¥πΑΗ
œύΙΊΧβΡΩ
œ¬Ν–ΆΦ–Έ÷–Θ§≤Μ «÷αΕ‘≥ΤΆΦ–ΈΒΡ «Θ®ΓΓΓΓΘ©
AΓΔ |
BΓΔ |
CΓΔ |
DΓΔ |
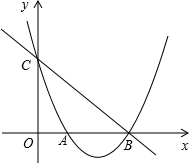 »γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒxOy÷–Θ§≈ΉΈοœΏy=x2+bx+c”κy÷αΫΜ”ΎΒψCΘ§”κx÷αΫΜ”ΎAΘ§BΝΫΒψΘ§ΒψBΒΡΉχ±ξΈΣBΘ®3Θ§0Θ©Θ§÷±œΏy=-x+3«ΓΚΟΨ≠ΙΐBΘ§CΝΫΒψΘ°
»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒxOy÷–Θ§≈ΉΈοœΏy=x2+bx+c”κy÷αΫΜ”ΎΒψCΘ§”κx÷αΫΜ”ΎAΘ§BΝΫΒψΘ§ΒψBΒΡΉχ±ξΈΣBΘ®3Θ§0Θ©Θ§÷±œΏy=-x+3«ΓΚΟΨ≠ΙΐBΘ§CΝΫΒψΘ° »γΆΦΘ§‘ΎΓςABC÷–Θ§ΓœC=90ΓψΘ§AD «ΓœBACΒΡΤΫΖ÷œΏΘ§CD=
»γΆΦΘ§‘ΎΓςABC÷–Θ§ΓœC=90ΓψΘ§AD «ΓœBACΒΡΤΫΖ÷œΏΘ§CD=