题目内容
5. 阅读理解:我们知道,任意两点关于它们所连线段的中点成中心对称,在平面直角坐标系中,任意两点P(x1,y1)、Q(x2,y2)的对称中心的坐标为($\frac{{x}_{1}+{x}_{2}}{2}$,$\frac{{y}_{1}+{y}_{2}}{2}$).
阅读理解:我们知道,任意两点关于它们所连线段的中点成中心对称,在平面直角坐标系中,任意两点P(x1,y1)、Q(x2,y2)的对称中心的坐标为($\frac{{x}_{1}+{x}_{2}}{2}$,$\frac{{y}_{1}+{y}_{2}}{2}$).观察应用:
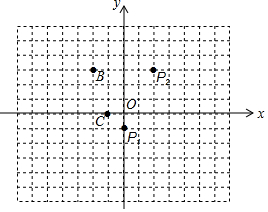
(1)如图,在平面直角坐标系中,若点P1(0,-1)、P2(2,3)的对称中心是点A,则点A的坐标为(1,1);
(2)另取两点B(-1.6,2.1)、C(-1,0).有一电子青蛙从点P1处开始依次关于点A、B、C作循环对称跳动,即第一次跳到点P1关于点A的对称点P2处,接着跳到点P2关于点B的对称点P3处,第三次再跳到点P3关于点C的对称点P4处,第四次再跳到点P4关于点A的对称点P5处,…则点P3、P8的坐标分别为(-5.2,1.2)、(2,3).
拓展延伸:
(3)求出点P2017的坐标,并直接写出在x轴上与点P2017,点C构成等腰三角形的点的坐标.
分析 (1)直接利用题目所给公式即可求出点A的坐标;
(2)首先利用题目所给公式求出P2的坐标,然后利用公式求出对称点P3的坐标,依此类推即可求出P8的坐标;
(3)由于P1(0,-1)→P2(2,3)→P3(-5.2,1.2)→P4(3.2,-1.2)→P5(-1.2,3.2)→P6(-2,1)→P7(0,-1)→P8(2,3),由此得到P7的坐标和P1的坐标相同,P8的坐标和P2的坐标相同,即坐标以6为周期循环,利用这个规律即可求出点P2017的坐标,也可以根据图形求出在x轴上与点P2017、点C构成等腰三角形的点的坐标.
解答 解:(1)点A的坐标为(1,1);
(2)P3、P8的坐标分别为(-5.2,1.2),(2,3);
(3)∵P1(0,-1)→P2(2,3)→P3(-5.2,1.2)→P4(3.2,-1.2)→P5(-1.2,3.2)→P6(-2,1)→P7(0,-1)→P8(2,3);
∴P7的坐标和P1的坐标相同,P8的坐标和P2的坐标相同,即坐标以6为周期循环.
∵2017÷6=336…1.
∴P2017的坐标与P1的坐标相同,为P2017(0,-1);
在x轴上与点P2017、点C构成等腰三角形的点的坐标为(-1-$\sqrt{2}$,0),(0,0),($\sqrt{2}$-1,0),(1,0).
故答案为:(1,1);(-5.2,1.2),(2,3).
点评 考查了坐标与图形变化-旋转,规律型:点的坐标,等腰三角形的判定,此题是一个阅读材料的题目,读懂题目,利用题目所给公式是解题的关键,利用公式可以解决后面的所有问题.

练习册系列答案
相关题目
13.某运动员在一场篮球比赛中的技术统计如表所示:
注:表中投中次数不包括罚球(只包括2分球和3分球)
根据以上信息,求本场比赛中该运动员投中2分球和3分球各几个.
| 技术 | 投中(次) | 罚球得分 | 个人总得分 |
| 数据 | 22 | 10 | 60 |
根据以上信息,求本场比赛中该运动员投中2分球和3分球各几个.

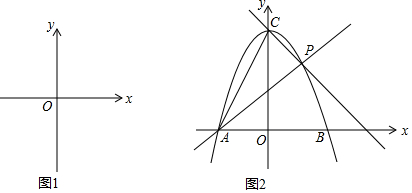
 如图,在矩形ABCD中,AB=4,BC=3,点P是矩形ABCD内的一个动点,且∠APB=90°,连接PC,若PC的长为整数,则PC的长可能为2或3或4.
如图,在矩形ABCD中,AB=4,BC=3,点P是矩形ABCD内的一个动点,且∠APB=90°,连接PC,若PC的长为整数,则PC的长可能为2或3或4.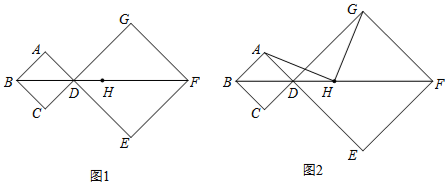
 已知,如图,正方形ABCD的边长为12,菱形EFGH的三个顶点E,G,H分别在正方形ABCD的边AB,CD,DA上,AH=4,连接CF.
已知,如图,正方形ABCD的边长为12,菱形EFGH的三个顶点E,G,H分别在正方形ABCD的边AB,CD,DA上,AH=4,连接CF.