��Ŀ����
10�� ֱ��y=-$\frac{\sqrt{3}}{3}$x+3��x�ᡢy��Ľ���ֱ�ΪB��C����A�������ǣ�-$\sqrt{3}$��0������һ��ֱ�߾�����A��C��
ֱ��y=-$\frac{\sqrt{3}}{3}$x+3��x�ᡢy��Ľ���ֱ�ΪB��C����A�������ǣ�-$\sqrt{3}$��0������һ��ֱ�߾�����A��C����1�����߶�AC����Ӧ�ĺ�������ʽ��
��2������M��B������BC�˶����ٶ�Ϊ1��һ����λ���ȣ�����M�˶���C��ʱֹͣ�˶�����M�˶�t��ʱ����ABM�����ΪS��
����S��t�ĺ�����ϵʽ��
�ڵ�tΪ��ֵʱ��S=$\frac{1}{2}$S��ABC����ע��S��ABC��ʾ��ABC��������������Ӧ��tֵ��
�۵�t=4��ʱ�������������Ƿ���ڵ�P��ʹ�á�BMP����BMΪֱ�DZߵ�ֱ�������Σ������ڣ���ֱ��д��P�����꣬�������ڣ���˵�����ɣ�
���� ��1�����ݺ���ֵ���ɵ���Ӧ�Ա�����ֵ�������Ա�����ֵ���ɵ���Ӧ�ĺ���ֵ�����ݴ���ϵ�������ɵú�������ʽ��
��2���ٸ���M���˶�ʱ�估�˶��ٶȣ��ɵ�BM�ij����������к���ֵ���ɵá�B�Ĵ�С���ٸ������Һ������ɵ�MD�ij��������߶εĺͲ�ɵ�AB�ij������������ε������ʽ���ɵô𰸣�
�ڸ��ݵȵ�������������S=$\frac{1}{2}$S��ABC�Ĺ�ϵ���ɵ�MD=$\frac{1}{2}$OB���ɵô𰸣�
�۸������⣬������������ٵ�P��x����ʱ���ڵ�P��y���ϣ���BPΪб��ʱ���۵�P��y���ϣ���BPΪ��һ��ֱ�DZ�ʱ��Ȼ�����ֱ�������ε����ʷ������ۣ����P��������Ƕ��ټ��ɣ�
��� �⣺��1����y=0ʱ��-$\frac{\sqrt{3}}{3}$x+3=0�����x=3$\sqrt{3}$����B��3$\sqrt{3}$��0��
��x=0ʱ��y=3����C�������ǣ�0��3��
���߶�AC����Ӧ�ĺ�������ʽy=kx+b��ͼ��A��C�㣬��$\left\{\begin{array}{l}{-\sqrt{3}k+b=0}\\{b=3}\end{array}\right.$��
���$\left\{\begin{array}{l}{k=\sqrt{3}}\\{b=3}\end{array}\right.$��
���߶�AC����Ӧ�ĺ�������ʽy=$\sqrt{3}$x+3��
��2����ͼ1��
���ɶ���M��B������BC�˶����ٶ�Ϊ1��һ����λ���ȣ���ʻt�룬��BM=t��
���߶εĺͲ��AB=3$\sqrt{3}$-��-$\sqrt{3}$��=4$\sqrt{3}$��
�����к�������tan��B=$\frac{OC}{OB}$=$\frac{3}{3\sqrt{3}}$=$\frac{\sqrt{3}}{3}$����ABC=30�㣬
�����Һ�������MD=BM•sin��ABC=$\frac{1}{2}$t��
�������������ʽ����S=$\frac{1}{2}$AB•MD=$\frac{1}{2}$��$\frac{1}{2}$t��4$\sqrt{3}$=$\sqrt{3}$t
��S=$\sqrt{3}$t��
����S=$\frac{1}{2}$S��ABC����MD=$\frac{1}{2}$OC=$\frac{3}{2}$����$\frac{1}{2}$t=$\frac{3}{2}$�����t=3��
��t=3ʱ��S=$\frac{1}{2}$S��ABC��
����ͼ2����t=4ʱ�����������ϴ��ڵ�P��ʹ�á�BMP����BMΪֱ�DZߵ�ֱ�������Σ�
����ͼ2��
�ߵ�M�˶����ٶ�Ϊÿ��1����λ���ȣ�
�൱t=4ʱ��BM=4��
�ߡ�ABC=30�㣬��PMB=90�㣬
��BP=BM��cos30��=4��$\frac{\sqrt{3}}{2}$=$\frac{8\sqrt{3}}{3}$��
��OP=OB-BP=3$\sqrt{3}$-$\frac{8\sqrt{3}}{3}$=$\frac{\sqrt{3}}{3}$��
���P�������ǣ�$\frac{\sqrt{3}}{3}$��0����
����ͼ3��PM��AB�ཻ�ڵ�N�� ��
��
�ߵ�M�˶����ٶ�Ϊÿ��1����λ���ȣ�
�൱t=4ʱ��BM=4��
�ߡ�ABC=30�㣬��NMB=90�㣬
��BN=BM��cos30��=4��$\frac{\sqrt{3}}{2}$=$\frac{8\sqrt{3}}{3}$��
��ON=OB-BN=3$\sqrt{3}$-$\frac{8\sqrt{3}}{3}$=$\frac{\sqrt{3}}{3}$��
�ߡ�MNB=90��-30��=60�㣬��ONP=��MNB��
���ONP=60�㣬
��OP=ON•tan60��=$\frac{\sqrt{3}}{3}��\sqrt{3}$=1��
���P�������ǣ�0��-1����
����ͼ4�� ��
��
��OC=3����ABC=30�㣬��BOC=90�㣬
��BC=2��3=6����PCB=90��-30��=60�㣬
�֡ߡ�PBC=90�㣬
���BPC=90��-60��=30�㣬
��CP=2BC=2��6=12��
��OP=CP-OC=12-3=9��
���P�������ǣ�0��-9����
���ϣ��ɵ�
��t=4ʱ�����������ϴ��ڵ�P��ʹ�á�BMP����BMΪֱ�DZߵ�ֱ�������Σ�
��P�������ǣ�$\frac{\sqrt{3}}{3}$��0������0��-1����0��-9����
���� ������һ�κ����ۺ��⣬��Ҫ������һ�κ������ۺ��⣬���ô���ϵ������������ʽ�����������������������˷�������˼���Ӧ�ã����ν��˼���Ӧ�ã�ֱ�������ε����ʺ�Ӧ�ã��Լ������ε��������Ҫ�������գ�

 ȫ�ŵ�����Ԫ�ƻ�ϵ�д�
ȫ�ŵ�����Ԫ�ƻ�ϵ�д�| ��һ�� | �ڶ��� | |
| ���ֻ��������� | 2 | 5 |
| ���ֻ��������� | 3 | 6 |
| �ۼ��˻����֣� | 13 | 28 |
��2����������Ҫ���øù�˾�ļ��ֻ���8�������ֻ���6�����պ�������������簴ÿ�ָ��˷�50Ԫ�������Ӧ���˷��ܶ�Ϊ����Ԫ��
��3������������20�ֻ����ƻ����øù�˾�Ļ������ã�ÿ���������أ������������꣬��������˾�����ļ����˻�������
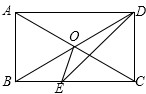 ��ͼ������ABCD�У�AC��BD���ڵ�O����AOB=60�㣬DEƽ�֡�ADC��BC�ڵ�E������OE�����COE=75�㣮
��ͼ������ABCD�У�AC��BD���ڵ�O����AOB=60�㣬DEƽ�֡�ADC��BC�ڵ�E������OE�����COE=75�㣮 ��ͼ���ı���ABCD�������Σ�CF��BD��DF��BE����BE=BD�����CDF=105�㣮
��ͼ���ı���ABCD�������Σ�CF��BD��DF��BE����BE=BD�����CDF=105�㣮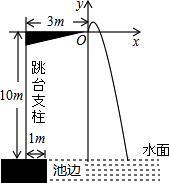 ��ͼ��2016����Լ���˻��ϣ�ij�˶�Ա��10����̨��ˮ����ʱ�������壨����һ�㣩�ڿ��е��˶�·����������y=-$\frac{25}{6}$x2+$\frac{10}{3}$x��ͼ�б��������Ϊ��֪���������˶�Ա�ڿ����˶������߶���ˮ��Ϊ$10\frac{2}{3}$�ף�
��ͼ��2016����Լ���˻��ϣ�ij�˶�Ա��10����̨��ˮ����ʱ�������壨����һ�㣩�ڿ��е��˶�·����������y=-$\frac{25}{6}$x2+$\frac{10}{3}$x��ͼ�б��������Ϊ��֪���������˶�Ա�ڿ����˶������߶���ˮ��Ϊ$10\frac{2}{3}$�ף�