题目内容
17.已知点O是直线AB上一点,∠COD是直角,OE平分∠BOC.(1)如图1,若∠AOC=40°,求∠DOE的度数;
(2)在图1中,若∠AOC=α,请直接写出∠DOE的度数(用含α的代数式表示);
(3)将图1中的∠COD按顺时针方向旋转至图2所示的位置,探究∠AOC与∠DOE的度数之间的关系,写出你的结论,并说明理由.

分析 (1)先求得∠BOC,再根据角平分线的性质得出∠COE,根据余角的性质得出∠DOE的度数;
(2)把数字换成希腊字母表示,同(1)的方法即可得出∠DOE的度数(用含α的代数式表示);
(3)结论是:∠DOE=$\frac{1}{2}$∠AOC.由平角的定义得出∠AOC+∠BOC=180°,再根据角平分线的性质得出∠COE=$\frac{1}{2}$∠BOC,即可代换出∠AOC与∠DOE的关系.
解答 解:(1)∵∠AOC+∠BOC=180°,
∴∠BOC=180°-∠AOC=180°-40°=140°,
∵OE平分∠BOC,
∴∠COE=$\frac{1}{2}$∠BOC=$\frac{1}{2}$×140°=70°,
∵∠COD是直角,∴∠COE+∠DOE=90°,
∴∠DOE=90°-∠COE=90°-70°=20°.
(2)若∠AOC=α,则∠DOE=$\frac{1}{2}$∠AOC=$\frac{α}{2}$.
(3)结论是:∠DOE=$\frac{1}{2}$∠AOC.
理由是:∵∠AOC+∠BOC=180°,
∴∠BOC=180°-∠AOC,
∵OE平分∠BOC,
∴∠COE=$\frac{1}{2}$∠BOC,
∵∠COD是直角,
∴∠COE+∠DOE=90°,
∴∠DOE=90°-∠COE=90°-$\frac{1}{2}$∠BOC
=90°-$\frac{1}{2}$(180°-∠AOC)
=$\frac{1}{2}$∠AOC.
点评 本题考查了角平分线的定义,是基础题,难度不大,掌握各角之间的关系是解题的关键.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案 培优三好生系列答案
培优三好生系列答案
相关题目
7.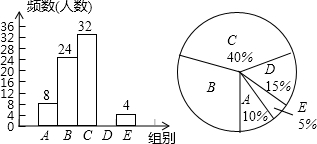 网络技术的发展对学生学习方式产生巨大的影响,某校为了解学生每周课余利用网络资源进行自主学习的时间,在本校随机抽取若干名学生进行问卷调查,下面是根据调查结果绘制成的不完整的统计图表:
网络技术的发展对学生学习方式产生巨大的影响,某校为了解学生每周课余利用网络资源进行自主学习的时间,在本校随机抽取若干名学生进行问卷调查,下面是根据调查结果绘制成的不完整的统计图表:
请根据图表中的信息解答下列问题:
(1)表中的n=12,扇形统计图中B组对应的圆心角为108°;
(2)请补全频数分布直方图;
(3)该校准备召开利用网络资源进行自主学习的交流会,计划在E组学生中随机选出两人进行经验介绍,已知E组的四名学生中,七、八年级各有1人,九年级有2人,请用画树状图法或列表法求抽取的两名学生都来自九年级的概率.
 网络技术的发展对学生学习方式产生巨大的影响,某校为了解学生每周课余利用网络资源进行自主学习的时间,在本校随机抽取若干名学生进行问卷调查,下面是根据调查结果绘制成的不完整的统计图表:
网络技术的发展对学生学习方式产生巨大的影响,某校为了解学生每周课余利用网络资源进行自主学习的时间,在本校随机抽取若干名学生进行问卷调查,下面是根据调查结果绘制成的不完整的统计图表:请根据图表中的信息解答下列问题:
| 组别 | 学习时间x(h) | 频数(人数) |
| A | 0<x≤1 | 8 |
| B | 1<x≤2 | 24 |
| C | 2<x≤3 | 32 |
| D | 3<x≤4 | n |
| E | 4小时以上 | 4 |
(2)请补全频数分布直方图;
(3)该校准备召开利用网络资源进行自主学习的交流会,计划在E组学生中随机选出两人进行经验介绍,已知E组的四名学生中,七、八年级各有1人,九年级有2人,请用画树状图法或列表法求抽取的两名学生都来自九年级的概率.
9.下列说法正确的是( )
| A. | 40°50′=40.5° | |
| B. | 若线段AP=BP,则P一定是AB中点 | |
| C. | 若∠AOC=$\frac{1}{2}$∠AOB,则OC是∠AOB的平分线 | |
| D. | 连结两点的线段的长度叫做两点之间的距离 |
 抛物线y=x2+4ax+b与x轴相交于O、A两点(其中O为坐标原点),过点P(2,2a)作直线PM⊥x轴于点M,交抛物线于点B,点B关于抛物线对称轴的对称点为C(其中B、C不重合),连接AP交y轴于点N,连接BC和PC.
抛物线y=x2+4ax+b与x轴相交于O、A两点(其中O为坐标原点),过点P(2,2a)作直线PM⊥x轴于点M,交抛物线于点B,点B关于抛物线对称轴的对称点为C(其中B、C不重合),连接AP交y轴于点N,连接BC和PC.