题目内容
在△ABC中,已知AB=6,BC=3,CA=4,任取AB上一点M,作MP∥AC,MQ∥BC.设AM=x,?MPCQ的周长为y,求出y关于x的函数关系式和自变量x的取值范围.
考点:相似三角形的判定与性质
专题:
分析:根据题意画出图形,由MP∥AC,MQ∥BC可以得到相应的线段成比例,根据比例式得到y与x的关系式.
解答: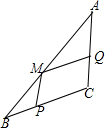 解:根据题意画出图形得到:
解:根据题意画出图形得到:
∵MP∥AC,MQ∥BC
∴
=
,
=
,
∴
=
,
=
,
∴MQ=
x,MP=4-
x,
∴y=2(MQ+MP)=2(
x+4-
x)=-
x+8,
∵0<x<6 MQ=
>0,MP=4-
x>0,
∴0<x<6.
 解:根据题意画出图形得到:
解:根据题意画出图形得到:∵MP∥AC,MQ∥BC
∴
| AM |
| AB |
| MQ |
| BC |
| BM |
| BA |
| MP |
| AC |
∴
| x |
| 6 |
| MQ |
| 3 |
| 6-x |
| 6 |
| MP |
| 4 |
∴MQ=
| 1 |
| 2 |
| 2 |
| 3 |
∴y=2(MQ+MP)=2(
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 3 |
∵0<x<6 MQ=
| x |
| 2 |
| 2 |
| 3 |
∴0<x<6.
点评:本题考查的是相似形综合题,此题涉及到相似三角形的判定和性质、平行线分线段成比例定理,函数思想和分类思想,数形结合思想是解答本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
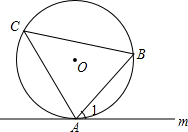 如图,直线m与⊙O相切于点A,∠C是弦AB所对的圆周角,试判断∠C与∠1的大小关系.
如图,直线m与⊙O相切于点A,∠C是弦AB所对的圆周角,试判断∠C与∠1的大小关系. 已知线段a,b,c.
已知线段a,b,c.
 如图,在菱形ABCD中,点E,F分别为边BC,CD的中点,连接AE,AF.
如图,在菱形ABCD中,点E,F分别为边BC,CD的中点,连接AE,AF. 如图,AB∥CD,∠A=38°,∠C=80°,求∠M.
如图,AB∥CD,∠A=38°,∠C=80°,求∠M.