题目内容
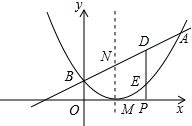 已知二次函数的图象的顶点坐标为M(1,0),直线y=x+m与该二次函数的图象交于A,B两点,其中A点的坐标为(3,4),B点在y轴上.
已知二次函数的图象的顶点坐标为M(1,0),直线y=x+m与该二次函数的图象交于A,B两点,其中A点的坐标为(3,4),B点在y轴上.(1)求m的值及这个二次函数的解析式;
(2)连结BM,AM,求出△MAB的面积;
(3)若P(a,0)是x轴上的一个动点,过P作x轴的垂线分别与直线AB和二次函数的图象交于D,E两点.
①当0<a<3时,求线段DE的最大值;
②若直线AB与抛物线的对称轴交点为N,问是否存在一点P,使以M、N、D、E为顶点的四边形是平行四边形?若存在,请求出此时P点的坐标;若不存在,请说明理由.
考点:二次函数综合题
专题:
分析:(1)将A点坐标分别代入抛物线的直线,便可求出抛物线的解析式和m的值;
(2)过A作AH⊥PM于H,利用△MAB的面积=S梯形BOHA-S△BOM-S△AMH计算即可;
(3)①线段DE的长为h,根据P点坐标分别求出DE两点坐标,便可求出h与a之间的函数关系式,进而可求出线段DE的最大值;
②存在一点P,使以M、N、D、E为顶点的四边形是平行四边形,要使四边形NMED是平行四边形,必须DE=MN=2,由①知DE=|-a2+3a|,进而求出a的值,所以P的坐标可求出.
(2)过A作AH⊥PM于H,利用△MAB的面积=S梯形BOHA-S△BOM-S△AMH计算即可;
(3)①线段DE的长为h,根据P点坐标分别求出DE两点坐标,便可求出h与a之间的函数关系式,进而可求出线段DE的最大值;
②存在一点P,使以M、N、D、E为顶点的四边形是平行四边形,要使四边形NMED是平行四边形,必须DE=MN=2,由①知DE=|-a2+3a|,进而求出a的值,所以P的坐标可求出.
解答:解:(1)设抛物线的解析式为y=a(x-1)2,
∵点A(3,4)在抛物线上,则4=a(3-1)2,
解得a=1,
∴抛物线的解析式为y=(x-1)2
∵点A(3,4)也在直线y=x+m,即4=3+m,
解得m=1;
(2)过A作AH⊥PM于H,
∵B(0,1),M(1,0),A(3,4),
∴OB=1,OH=3,AH=4,
∴△MAB的面积=S梯形BOHA-S△BOM-S△AMH=7.5-
×1×1-
×2×4=3;
(3)①已知P点坐标为P(a,0),则E点坐标为E(a,a2-2a+1),D点坐标为D(a,a+1),
h=DE=yD-yE=a+1-(a2-2a+1)=-a2+3a,
∴h与a之间的函数关系式为h=-a2+3a=-(a-
)2+
(0<a<3),
∴线段DE的最大值是
;
②存在一点P,使以M、N、D、E为顶点的四边形是平行四边形,
理由是∵M(1,0),
∴把x=1代入y=x+1得:y=2,
即N(1,2),
∴MN=2,
要使四边形NMED是平行四边形,必须DE=MN=2,
由①知DE=|-a2+3a|,
∴2=|-a2+3a|,
解得:a1=2,a2=1,a3=
,a4=
,
∴(2,0),(1,0)(因为和M重合,舍去)(
,0),(
,0)
∴P的坐标是(2,0),(
,0),(
,0).
∵点A(3,4)在抛物线上,则4=a(3-1)2,
解得a=1,
∴抛物线的解析式为y=(x-1)2
∵点A(3,4)也在直线y=x+m,即4=3+m,

解得m=1;
(2)过A作AH⊥PM于H,
∵B(0,1),M(1,0),A(3,4),
∴OB=1,OH=3,AH=4,
∴△MAB的面积=S梯形BOHA-S△BOM-S△AMH=7.5-
| 1 |
| 2 |
| 1 |
| 2 |
(3)①已知P点坐标为P(a,0),则E点坐标为E(a,a2-2a+1),D点坐标为D(a,a+1),
h=DE=yD-yE=a+1-(a2-2a+1)=-a2+3a,
∴h与a之间的函数关系式为h=-a2+3a=-(a-
| 3 |
| 2 |
| 9 |
| 4 |
∴线段DE的最大值是
| 9 |
| 4 |
②存在一点P,使以M、N、D、E为顶点的四边形是平行四边形,
理由是∵M(1,0),
∴把x=1代入y=x+1得:y=2,
即N(1,2),
∴MN=2,
要使四边形NMED是平行四边形,必须DE=MN=2,
由①知DE=|-a2+3a|,
∴2=|-a2+3a|,
解得:a1=2,a2=1,a3=
3+
| ||
| 2 |
3-
| ||
| 2 |
∴(2,0),(1,0)(因为和M重合,舍去)(
3+
| ||
| 2 |
3-
| ||
| 2 |
∴P的坐标是(2,0),(
3+
| ||
| 2 |
3-
| ||
| 2 |
点评:本题是二次函数的综合题,其中涉及到的知识点有抛物线的公式的求法和三角形的性质等知识点,是各地中考的热点和难点,解题时注意数形结合数学思想的运用,同学们要加强训练,属于中档题.

练习册系列答案
相关题目
 如图,按此规律,第6行最后一个数字是
如图,按此规律,第6行最后一个数字是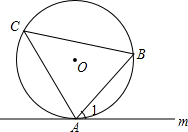 如图,直线m与⊙O相切于点A,∠C是弦AB所对的圆周角,试判断∠C与∠1的大小关系.
如图,直线m与⊙O相切于点A,∠C是弦AB所对的圆周角,试判断∠C与∠1的大小关系.