题目内容
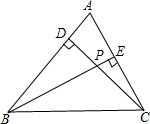如图，在锐角三角形ABC中，CD、BE分别是AB、AC边上的高，且CD、BE交于一点P，若∠A=50°，求∠BPC的度数．
解：∵∠A=50°，BE⊥AC，
∴∠ABE=90°-50°=40°，
又∵CD⊥AB，
∴∠BPC=90°+∠ABE=130°．
分析：首先根据直角三角形的两个锐角互余，求得∠ABE的度数，再根据三角形的内角和定理的推论进行求解．
点评：考查了三角形的内角和定理以及三角形的外角性质．
∴∠ABE=90°-50°=40°，
又∵CD⊥AB，
∴∠BPC=90°+∠ABE=130°．
分析：首先根据直角三角形的两个锐角互余，求得∠ABE的度数，再根据三角形的内角和定理的推论进行求解．
点评：考查了三角形的内角和定理以及三角形的外角性质．
练习册系列答案
相关题目
（1）如图，在锐角三角形ABC中，BC=12，
如图，在锐角三角形ABC中，AD⊥BC，AD=12，AC=13，BC=14．则AB=
如图，在锐角三角形ABC中，AD⊥BC，AD=12cm，AB=13cm，BC=14cm，则AC的长为（ ）| A、12cm | B、13cm | C、14cm | D、15cm |
如图，在锐角三角形ABC中，AD、CE分别是边BC、AB上的高，垂足分别是D、E，AD、CE相交于点O，若∠B=60°，则∠AOE的度数是（ ）
如图，在锐角三角形ABC中，BC=