题目内容
（1）如图，在锐角三角形ABC中，BC=12，sinA=| 3 | 4 |
（2）若BC=a、CA=b、AB=c，sinA、sinB、sinC分别表示三个锐角的正弦值，三角形的外接圆的半径为R，反思（1）的解题过程，请你猜想并写出一个结论．（不需证明）
分析：（1）根据直径所对的圆周角是直角，构造直角三角形，根据锐角三角函数的定义求解；
（2）根据（1）的解题过程，把已知数字换成字母就可．
（2）根据（1）的解题过程，把已知数字换成字母就可．
解答：
解：（1）连接CO并延长交圆O于点D，连接BD；
∵∠A与∠D均为弧BC所对的圆周，
∴∠A=∠D，sinA=sinD=
，
∵CD为圆的直径，
∴∠DBC=90°；
∵在Rt△DBC中，sinD=
，
∴CD=
=16，
所以，此三角形的外接圆的半径为8．
（2）
=
=
=2R．
解：（1）连接CO并延长交圆O于点D，连接BD；∵∠A与∠D均为弧BC所对的圆周，
∴∠A=∠D，sinA=sinD=
| 3 |
| 4 |
∵CD为圆的直径，
∴∠DBC=90°；
∵在Rt△DBC中，sinD=
| BC |
| CD |
∴CD=
| BC |
| sinD |
所以，此三角形的外接圆的半径为8．
（2）
| a |
| sinA |
| b |
| sinB |
| c |
| sinC |
点评：此题实际上是正弦定理的证明过程．注意在圆中，利用直径构造直角．
练习册系列答案
阅读快车系列答案
相关题目
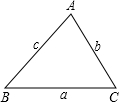如图，在锐角△ABC中，a＞b＞c，以某任意两个顶点为顶点作矩形，第三个顶点落在以这两个顶点所确定的对边上，这样可以作三个面积相等的矩形，请问这三个矩形的周长大小关系如何？（记ta、tb、tc分别以a、b、c为边的矩形的周长）答：
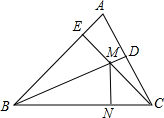如图，在锐角△ABC中，∠ABC的平分线交AC于点D，AB边上的高CE交BD于点M，过点M作BC的垂线段MN，若EC=4，∠BCE=45°，则MN=
