Question

如图，在锐角三角形ABC中，BC=4

2

，∠ABC=45°，BD平分∠ABC，M、N分别是BD、BC上的动点，试求CM+MN的最小值．

Answer 1

分析：过点C作CE⊥AB于点E，交BD于点M′，过点M′作M′N′⊥BC于N′，则CE即为CM+MN的最小值，再根据BC=4

2

，∠ABC=45°，BD平分∠ABC可知△BCE是等腰直角三角形，由锐角三角函数的定义即可求出CE的长．

解答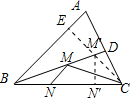：解：过点C作CE⊥AB于点E，交BD于点M′，过点M′作M′N′⊥BC于N′，则CE即为CM+MN的最小值，
∵BC=4

2

，∠ABC=45°，BD平分∠ABC，
∴△BCE是等腰直角三角形，
∴CE=BC•cos45°=4

2

×

2

2

=4．
故CM+MN的最小值为4．

点评：本题考查的是轴对称-最短路线问题，根据题意作出辅助线，构造出等腰直角三角形，利用锐角三角函数的定义求解是解答此题的关键．