题目内容
12.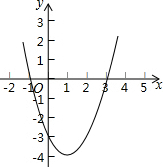 如图,是二次函数y=ax2+bx+c的图象,据图象中的有关信息,下列结论不成立的是( )
如图,是二次函数y=ax2+bx+c的图象,据图象中的有关信息,下列结论不成立的是( )| A. | a>0 | |
| B. | 对称轴是直线x=1 | |
| C. | c>0 | |
| D. | 一元二次方程ax2+bx+c=0有两个不相等的实数根 |
分析 根据函数图象的开口方向可以确定a的正负,与y轴的交点可以确定c的正负,与x轴的交点可以确定一元二次方程ax2+bx+c=0的根的情况,根据二次函数图象具有对称性可以得到二次函数的对称轴.
解答 解:根据函数图象开口向上可知a>0,故选项A正确;
根据函数图象与x轴交于点(-1,0)与(3,0),可得二次函数的对称轴为:x=$\frac{(-1)+3}{2}$=1,故选线B正确;
根据二次函数与y轴交于负半轴可知c<0,故选项C错误;
二次函数与x轴交于点(-1,0)与(3,0),可知一元二次方程ax2+bx+c=0有两个不相等的实数根,故选项D正确.
故选:C.
点评 本题考查二次函数图象与系数的关系,通过图象给出的信息得到所要判断的结论是否正确.

练习册系列答案
相关题目
7.若(-7x2-5y)( )=49x4-25y2,括号内应填代数式( )
| A. | 7x2+5y | B. | -7x2-5y | C. | -7x2+5y | D. | 7x2-5y |
1.数轴上A,B,C三个点分别对应着a,b,c三个数,若a<b<c,且AC=2BC,则下列关系式成立的是( )
| A. | c=2a+b | B. | c=a+2b | C. | c=2b-a | D. | c=2a-b |
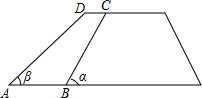 如图,沿水库拦水坝的背水坡将坝面加宽CD=2米,坡度由原来的$\sqrt{3}$:1改为1:1,已知背水坡BC长12米.
如图,沿水库拦水坝的背水坡将坝面加宽CD=2米,坡度由原来的$\sqrt{3}$:1改为1:1,已知背水坡BC长12米.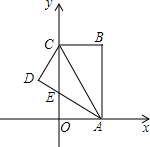 如图,长方形AB长为9,OA长为3,将长方形沿对角线AC折叠,使得点B与点D重合,且与y轴交于点E.
如图,长方形AB长为9,OA长为3,将长方形沿对角线AC折叠,使得点B与点D重合,且与y轴交于点E.