题目内容
1.数轴上A,B,C三个点分别对应着a,b,c三个数,若a<b<c,且AC=2BC,则下列关系式成立的是( )| A. | c=2a+b | B. | c=a+2b | C. | c=2b-a | D. | c=2a-b |
分析 根据a<b<c,且AC=2BC,所以点B为AC的中点,根据中点的定义得到b=$\frac{a+c}{2}$,即可解答.
解答 解:如图,
∵a<b<c,AC=2BC,
∴点B为AC的中点,
∴b=$\frac{a+c}{2}$,
∴c=2b-a,
故选:C.
点评 本题考查了数轴,解决本题的关键是借助于数轴明确点B为AC的中点.

练习册系列答案
相关题目
12.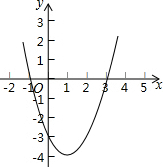 如图,是二次函数y=ax2+bx+c的图象,据图象中的有关信息,下列结论不成立的是( )
如图,是二次函数y=ax2+bx+c的图象,据图象中的有关信息,下列结论不成立的是( )
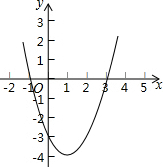 如图,是二次函数y=ax2+bx+c的图象,据图象中的有关信息,下列结论不成立的是( )
如图,是二次函数y=ax2+bx+c的图象,据图象中的有关信息,下列结论不成立的是( )| A. | a>0 | |
| B. | 对称轴是直线x=1 | |
| C. | c>0 | |
| D. | 一元二次方程ax2+bx+c=0有两个不相等的实数根 |
11.多项式-a2-1与3a2-2a+1的和为( )
| A. | 2a2-2a | B. | 4a2-2a+2 | C. | 4a2-2a-2 | D. | 2a2+2a |
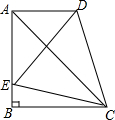 如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=BC,E为AB边上一点,∠BCE=15°,且AE=AD,连接DE交AC于H.下列结论:①△ACD≌△ACE;②∠ACD=30°;③A、C两点关于DE所在直线对称;④$\frac{{S}_{△AEH}}{{S}_{△CDH}}$=$\frac{EH}{CD}$.其中正确的结论是①②.(把你认为正确的结论的序号都填上)
如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=BC,E为AB边上一点,∠BCE=15°,且AE=AD,连接DE交AC于H.下列结论:①△ACD≌△ACE;②∠ACD=30°;③A、C两点关于DE所在直线对称;④$\frac{{S}_{△AEH}}{{S}_{△CDH}}$=$\frac{EH}{CD}$.其中正确的结论是①②.(把你认为正确的结论的序号都填上)