题目内容
3.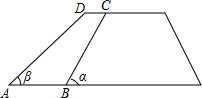 如图,沿水库拦水坝的背水坡将坝面加宽CD=2米,坡度由原来的$\sqrt{3}$:1改为1:1,已知背水坡BC长12米.
如图,沿水库拦水坝的背水坡将坝面加宽CD=2米,坡度由原来的$\sqrt{3}$:1改为1:1,已知背水坡BC长12米.(1)求原背水坡的坡角α和加宽后的坡角β的度数;
(2)求加宽后水坝的横截面面积增加了多少?
分析 (1)过点C作CE⊥AB于E,过点D作DF⊥AB于F,根据加宽前后的坡度求出坡角;
(2)在△BCE和△ADF中分别利用三角函数的知识求出CE、BE、AF的长度,进而可求出横截面积.
解答 解:(1)过点C作CE⊥AB于E,过点D作DF⊥AB于F,
∵tanα=$\sqrt{3}$,tanβ=1,
∴α=60°,β=45°;
(2)在Rt△BCE中,
∵$\frac{CE}{12}$=sin60°,$\frac{BE}{12}$=cos60°,
∴CE=6$\sqrt{3}$,BE=6,BF=BE-EF=4,
在Rt△ADF中,
∵DF=6$\sqrt{3}$,且$\frac{6\sqrt{3}}{AF}$=tan45°,
∴AF=6$\sqrt{3}$,
∴AB=6$\sqrt{3}$-4,
∴S四边形ABCD=$\frac{1}{2}$(2+6$\sqrt{3}$-4)×6$\sqrt{3}$=54-6$\sqrt{3}$(米2).
答:加宽后水坝的横截面面积增加了(54-6$\sqrt{3}$)米2.
点评 本题考查了解直角三角线的应用,解答本题的关键是根据所给的坡度求出坡角构造直角三角形,利用三角函数的知识求解.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
13.甲、乙两超市(大型商场)同时开业,为了吸引顾客,都举行有奖酬宾活动:凡购物满100元,均可得到一次摸奖的机会.在一个纸盒里装有2个红球和2个白球,除颜色外其它都相同,摸奖者一次从中摸出两个球,根据球的颜色决定送礼金券(在他们超市使用时,与人民币等值)的多少(如下表).
甲超市:
乙超市:
如果只考虑中奖因素,你将会选择去甲超市购物.请说明理由甲超市平均获得的礼金券钱数多.
甲超市:
| 球 | 两红 | 一红一白 | 两白 |
| 礼金券(元) | 5 | 10 | 5 |
| 球 | 两红 | 一红一白 | 两白 |
| 礼金券(元) | 10 | 5 | 10 |
15.解方程组$\left\{\begin{array}{l}{ax+by=2}\\{cx-7y=8}\end{array}\right.$时,一学生把c看错而得$\left\{\begin{array}{l}{x=-2}\\{y=2}\end{array}\right.$,而正确的解是$\left\{\begin{array}{l}{x=3}\\{y=-2}\end{array}\right.$,那么a、b、c的值是( )
| A. | 不能确定 | B. | 4,5,-2 | C. | 4,7,2 | D. | 4,7,-2 |
12.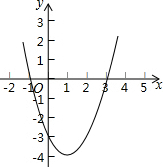 如图,是二次函数y=ax2+bx+c的图象,据图象中的有关信息,下列结论不成立的是( )
如图,是二次函数y=ax2+bx+c的图象,据图象中的有关信息,下列结论不成立的是( )
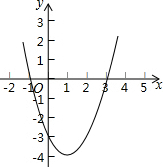 如图,是二次函数y=ax2+bx+c的图象,据图象中的有关信息,下列结论不成立的是( )
如图,是二次函数y=ax2+bx+c的图象,据图象中的有关信息,下列结论不成立的是( )| A. | a>0 | |
| B. | 对称轴是直线x=1 | |
| C. | c>0 | |
| D. | 一元二次方程ax2+bx+c=0有两个不相等的实数根 |
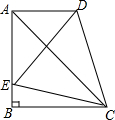 如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=BC,E为AB边上一点,∠BCE=15°,且AE=AD,连接DE交AC于H.下列结论:①△ACD≌△ACE;②∠ACD=30°;③A、C两点关于DE所在直线对称;④$\frac{{S}_{△AEH}}{{S}_{△CDH}}$=$\frac{EH}{CD}$.其中正确的结论是①②.(把你认为正确的结论的序号都填上)
如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=BC,E为AB边上一点,∠BCE=15°,且AE=AD,连接DE交AC于H.下列结论:①△ACD≌△ACE;②∠ACD=30°;③A、C两点关于DE所在直线对称;④$\frac{{S}_{△AEH}}{{S}_{△CDH}}$=$\frac{EH}{CD}$.其中正确的结论是①②.(把你认为正确的结论的序号都填上)