题目内容
20.计算(1)$-{1^2}-(\frac{1}{3}-\frac{1}{2})÷\frac{1}{3}×[-3-{(-2)^3}]$
(2)${(-0.125)^{2013}}×{8^{2012}}×[{(-5)^{11}}-4+{5^{11}}]-(\frac{1}{2}-\frac{2}{3}-\frac{1}{8})÷{(-\frac{1}{6})^2}$.
分析 (1)先算括号里面的,再算乘方,乘除,最后算加减即可;
(2)先算括号里面的,再根据乘法分配律进行计算即可.
解答 解:(1)原式=-1+$\frac{1}{6}$×3×(-3+8)
=-1+$\frac{1}{6}$×3×5
=-1+$\frac{5}{2}$
=$\frac{3}{2}$;
(2)原式=(-0.125×8)2012×(-0.125)×(-4)-($\frac{1}{2}$×36-$\frac{2}{3}$×36-$\frac{1}{8}$×36)
=-0.125×(-4)-(18-24-$\frac{9}{2}$)
=0.5+$\frac{21}{2}$
=11.
点评 本题考查的是有理数的混合运算,熟知有理数混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
15.解方程组$\left\{\begin{array}{l}{ax+by=2}\\{cx-7y=8}\end{array}\right.$时,一学生把c看错而得$\left\{\begin{array}{l}{x=-2}\\{y=2}\end{array}\right.$,而正确的解是$\left\{\begin{array}{l}{x=3}\\{y=-2}\end{array}\right.$,那么a、b、c的值是( )
| A. | 不能确定 | B. | 4,5,-2 | C. | 4,7,2 | D. | 4,7,-2 |
12.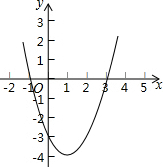 如图,是二次函数y=ax2+bx+c的图象,据图象中的有关信息,下列结论不成立的是( )
如图,是二次函数y=ax2+bx+c的图象,据图象中的有关信息,下列结论不成立的是( )
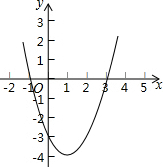 如图,是二次函数y=ax2+bx+c的图象,据图象中的有关信息,下列结论不成立的是( )
如图,是二次函数y=ax2+bx+c的图象,据图象中的有关信息,下列结论不成立的是( )| A. | a>0 | |
| B. | 对称轴是直线x=1 | |
| C. | c>0 | |
| D. | 一元二次方程ax2+bx+c=0有两个不相等的实数根 |
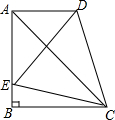 如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=BC,E为AB边上一点,∠BCE=15°,且AE=AD,连接DE交AC于H.下列结论:①△ACD≌△ACE;②∠ACD=30°;③A、C两点关于DE所在直线对称;④$\frac{{S}_{△AEH}}{{S}_{△CDH}}$=$\frac{EH}{CD}$.其中正确的结论是①②.(把你认为正确的结论的序号都填上)
如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=BC,E为AB边上一点,∠BCE=15°,且AE=AD,连接DE交AC于H.下列结论:①△ACD≌△ACE;②∠ACD=30°;③A、C两点关于DE所在直线对称;④$\frac{{S}_{△AEH}}{{S}_{△CDH}}$=$\frac{EH}{CD}$.其中正确的结论是①②.(把你认为正确的结论的序号都填上) 如图为一张方格纸,纸上有一灰色三角形,其顶点均位于某两网格线的交点上,若灰色三角形面积为$\frac{21}{4}$,则方格纸的面积为12.
如图为一张方格纸,纸上有一灰色三角形,其顶点均位于某两网格线的交点上,若灰色三角形面积为$\frac{21}{4}$,则方格纸的面积为12.