题目内容
20.某公司需要购买甲、乙两种商品共150件,甲、乙两种商品的价格分别为600元和1000元.且要求乙种商品的件数不少于甲种商品件数的2倍.设购买甲种商品x件,购买两种商品共花费y元.(1)请求出y与x的函数关系式及x的取值范围.
(2)试利用函数的性质说明,当购买多少件甲种商品时,所需要的费用最少?
分析 (1)设甲商品有x件,则乙商品则有(150-x)件,根据甲、乙两种商品共150件和乙种商品的件数不少于甲种商品件数的2倍,列出不等式组,求出x的取值范围,再根据甲、乙两种商品的价格列出一次函数关系式即可;
(2)根据(1)得出一次函数y随x的增大而减少,即可得出当x=50时,所需要的费用最少.
解答 解:(1)设甲商品有x件,则乙商品则有(150-x)件,根据题意得:
$\left\{\begin{array}{l}{150-x≥2x}\\{x≥0}\end{array}\right.$,
解得:0≤x≤50.
则y与x的函数关系式是:y=600x+1000(150-x)=-400x+150000(0≤x≤50);
(2)∵k=-400<0,
∴一次函数y随x的增大而减少,
∴当x=50时,y最小=-400×50+150000=130000(元).
答:购买50件甲种商品时,所需要的费用最少.
点评 本题考查了一次函数的应用,关键是根据商品的价格列出函数关系式,再根据题意求出自变量的取值范围.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
10.如果两个相似三角形的周长比为1:4,那么这两个三角形的相似比为( )
| A. | 1:2 | B. | 1:4 | C. | 1:8 | D. | 1:16 |
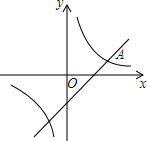 如图,在平面直角坐标系xOy中,双曲线y=$\frac{m}{x}$与直线y=kx-2交于点A(3,1).
如图,在平面直角坐标系xOy中,双曲线y=$\frac{m}{x}$与直线y=kx-2交于点A(3,1). 如图,EB是直径,O是圆心,CB,CD切半圆于B,D,CD交BE延长线于点A,若BC=6,AD=2AE,求半圆的面积.
如图,EB是直径,O是圆心,CB,CD切半圆于B,D,CD交BE延长线于点A,若BC=6,AD=2AE,求半圆的面积.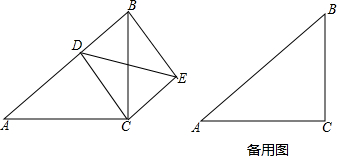
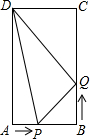 如图,在矩形ABCD中,AB=6cm,BC=12cm,点P从点A沿边AB向终点B以1cm/s的速度移动;同时,点Q从点B沿边BC向终点C以2cm/s的速度移动.设移动时间为t秒,解答下列问题:
如图,在矩形ABCD中,AB=6cm,BC=12cm,点P从点A沿边AB向终点B以1cm/s的速度移动;同时,点Q从点B沿边BC向终点C以2cm/s的速度移动.设移动时间为t秒,解答下列问题: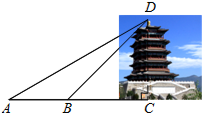 “永定楼”是门头沟区的地标性建筑,某中学九年级数学兴趣小组进行了测量它高度的社会实践活动.如图,他们在A点测得顶端D的仰角∠DAC=30°,向前走了46米到达B点后,在B点测得顶端D的仰角∠DBC=45°.求永定楼的高度CD.(结果保留根号)
“永定楼”是门头沟区的地标性建筑,某中学九年级数学兴趣小组进行了测量它高度的社会实践活动.如图,他们在A点测得顶端D的仰角∠DAC=30°,向前走了46米到达B点后,在B点测得顶端D的仰角∠DBC=45°.求永定楼的高度CD.(结果保留根号)