题目内容
15.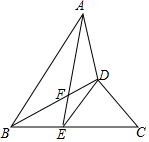 如图,线段BD平分∠ABC,且AB=BC,E是线段BC上一点,DE=DC,连接AE交BD于点F.
如图,线段BD平分∠ABC,且AB=BC,E是线段BC上一点,DE=DC,连接AE交BD于点F.(1)求证:△DAF∽△DBA;
(2)若点P是线段AF上一点,连结BP,若∠PBD=$\frac{1}{2}$∠BAD,AB=3,AD=2.求$\frac{EF}{FP}$.
分析 (1)由△DBA≌△DBC,推出DA=DC,∠C=∠BAD,由2∠DAE+∠ADE=180°,2∠ABD+∠ADE=180°,推出2∠DAE=2∠ABD,推出∠DAF=∠ABD,由∠ADF=∠BDA,
可得△DAF∽△DBA;
(2)由△DAF∽△DBA,推出∠AFD=∠BAD,$\frac{DF}{DA}$=$\frac{AF}{BA}$,由∠PBD=$\frac{1}{2}$∠BAD,AB=3,AD=2,推出∠PBD=$\frac{1}{2}$∠AFD,$\frac{AF}{DF}$=$\frac{AB}{AD}$=$\frac{3}{2}$,推出∠FPB=∠FBP,推出BF=PF,由∠BFE=∠AFD,∠FBE=∠FAD,推出△BFE∽△AFD,可得$\frac{EF}{BF}$=$\frac{DF}{AF}$=$\frac{2}{3}$;
解答 (1)证明:∵BD平分∠ABC,
∴∠DBA=∠DBC,
在△DBA和△DBC中,
$\left\{\begin{array}{l}{BD=BD}\\{∠DBA=∠DBC}\\{BA=BC}\end{array}\right.$,
∴△DBA≌△DBC,
∴DA=DC,∠C=∠BAD,
∵DE=DC,
∴DA=DE,∠C=∠DEC,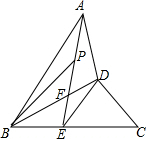
∴∠DAE=∠DEA,
∴2∠DAE+∠ADE=180°,
∵∠DEC+∠DEB=180°,
∴∠DEB+∠BAD=180°,
∴∠ABE+∠ADE=180°,
∴2∠ABD+∠ADE=180°,
∴2∠DAE=2∠ABD,
∴∠DAF=∠ABD,∵∠ADF=∠BDA,
∴△DAF∽△DBA.
(2)∵△DAF∽△DBA,
∴∠AFD=∠BAD,$\frac{DF}{DA}$=$\frac{AF}{BA}$,
∵∠PBD=$\frac{1}{2}$∠BAD,AB=3,AD=2,
∴∠PBD=$\frac{1}{2}$∠AFD,$\frac{AF}{DF}$=$\frac{AB}{AD}$=$\frac{3}{2}$,
∴∠FPB=∠FBP,
∴BF=PF,
∵∠BFE=∠AFD,∠FBE=∠FAD,
∴△BFE∽△AFD,
∴$\frac{EF}{BF}$=$\frac{DF}{AF}$=$\frac{2}{3}$,
∴$\frac{EF}{PF}$=$\frac{2}{3}$.
点评 本题主要考查了全等三角形的判定与性质、相似三角形的判定与性质、等腰三角形的判定与性质/多边形的内角和定理、三角形的外角性质等知识,证到∠ABE+∠ADE=180°是解决第(1)小题的关键,证到BF=PF是解决第(2)小题的关键.

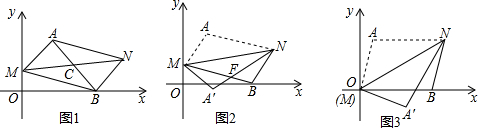
 △ABC在平面直角坐标系中的位置如图所示.
△ABC在平面直角坐标系中的位置如图所示.