题目内容
5.已知a+b=5,ab=6,那么a2+b2=13,a2-b2=±5.分析 (1)把a+b=5两边平方,利用完全平方公式化简,将ab的值代入计算即可求出原式的值;
(2)原式利用完全平方公式求出(a-b)的值,进而计算即可求出值.
解答 解:把a+b=5两边平方得:(a+b)2=a2+b2+2ab=25,
把ab=6代入得:a2+b2=13;
∵a2+b2=13,ab=6,
∴(a-b)2=a2+b2-2ab=13-12=1,
∴a-b=±1,
∴a2-b2=(a+b)(a-b)=±5.
故答案为:13,±5.
点评 此题考查了完全平方公式,熟练掌握完全平方公式是解本题的关键.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
10.多项式:①16x2-8x;②(x-1)2-4(x-1)2;③(x+1)4-4(x+1)2+4x2;④-4x2-1+4x分解因式后,结果中含有相同因式的是( )
| A. | ①和② | B. | ③和④ | C. | ①和④ | D. | ②和③ |
17.下列各式中,不能利用平方差公式因式分解的是( )
| A. | x2-y2 | B. | -x2+y2 | C. | 4x2y2-1 | D. | -x2-y2 |
 画出下图圆柱空心三菱柱的三视图(注:空心的部分是圆柱体)
画出下图圆柱空心三菱柱的三视图(注:空心的部分是圆柱体) 如图,使用圆规和直尺分别画出∠AOB和∠BOC的角平分线OM和ON,如果∠MON=68°,那么:
如图,使用圆规和直尺分别画出∠AOB和∠BOC的角平分线OM和ON,如果∠MON=68°,那么: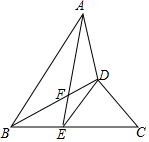 如图,线段BD平分∠ABC,且AB=BC,E是线段BC上一点,DE=DC,连接AE交BD于点F.
如图,线段BD平分∠ABC,且AB=BC,E是线段BC上一点,DE=DC,连接AE交BD于点F.