题目内容
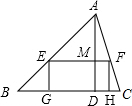 如图,矩形EFHG的边GH在△ABC边BC上,其他两个顶点分别在边AB、AC上,已知△ABC的边BC=120cm,BC边上的高AD为80cm;求:
如图,矩形EFHG的边GH在△ABC边BC上,其他两个顶点分别在边AB、AC上,已知△ABC的边BC=120cm,BC边上的高AD为80cm;求:(1)当矩形EFHG是正方形时,求这个正方形的边长;
(2)设EG的长为x cm,x为何值时,矩形EFHG的面积最大?并求面积的最大值.
考点:相似三角形的判定与性质,二次函数的最值
专题:
分析:(1)证明△AEF∽△ABC,列出比例式,即可解决问题.
(2)用变量x来表示EF的长度,进而表示出矩形EFHG的面积,即可解决问题.
(2)用变量x来表示EF的长度,进而表示出矩形EFHG的面积,即可解决问题.
解答: 解:(1)∵四边形EFHG是正方形,且AD⊥BC,
解:(1)∵四边形EFHG是正方形,且AD⊥BC,
∴EF∥BC,EG=EF=MD(设为λ),
∴△AEF∽△ABC,AM=80-λ;
∴EF:BC=AM:AD,
即λ:120=(80-λ):80,
解得:λ=48(cm),
即这个正方形的边长为48cm.
(2)设矩形EFHG的面积为λ,
由(1)知:EF:BC=AM:AD,
即EF:120=(80-x):80,
解得:EF=120-1.5x,
∴λ=x(120-1.5x)=-1.5x2+120x,
∴当x=-
=40时,λ取得最大值,
λ的最大值=-1.5×1600+120×40=2400(cm2).
 解:(1)∵四边形EFHG是正方形,且AD⊥BC,
解:(1)∵四边形EFHG是正方形,且AD⊥BC,∴EF∥BC,EG=EF=MD(设为λ),
∴△AEF∽△ABC,AM=80-λ;
∴EF:BC=AM:AD,
即λ:120=(80-λ):80,
解得:λ=48(cm),
即这个正方形的边长为48cm.
(2)设矩形EFHG的面积为λ,
由(1)知:EF:BC=AM:AD,
即EF:120=(80-x):80,
解得:EF=120-1.5x,
∴λ=x(120-1.5x)=-1.5x2+120x,
∴当x=-
| 120 |
| 2×(-1.5) |
λ的最大值=-1.5×1600+120×40=2400(cm2).
点评:该题主要考查了相似三角形的判定及其性质、二次函数的性质等数学知识点的应用问题;解题的关键是灵活运用有关定理来分析、判断、推理或解答;对综合运用能力提出了一定的要求.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
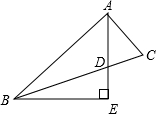 如图,AD是△ABC的角平分线,AD=AC,BE⊥AD于E
如图,AD是△ABC的角平分线,AD=AC,BE⊥AD于E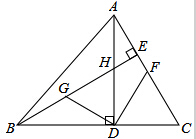 如图,△ABC中,AD、BE分别是BC、AC边上的高,且交于H,G为BH的中点,F为AC中点,且∠ABC=45°,求证:DG=DF,DG⊥DF.
如图,△ABC中,AD、BE分别是BC、AC边上的高,且交于H,G为BH的中点,F为AC中点,且∠ABC=45°,求证:DG=DF,DG⊥DF.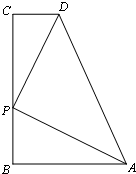 如图,已知四边形ABCD,∠B=∠C=90°,P是BC边上的一点,∠APD=90°.
如图,已知四边形ABCD,∠B=∠C=90°,P是BC边上的一点,∠APD=90°.