题目内容
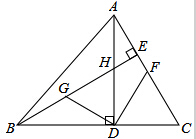 如图,△ABC中,AD、BE分别是BC、AC边上的高,且交于H,G为BH的中点,F为AC中点,且∠ABC=45°,求证:DG=DF,DG⊥DF.
如图,△ABC中,AD、BE分别是BC、AC边上的高,且交于H,G为BH的中点,F为AC中点,且∠ABC=45°,求证:DG=DF,DG⊥DF.考点:全等三角形的判定与性质
专题:证明题
分析:易证BD=AD和∠DBH=∠CAD,即可证明∴△CAD≌△HBD,可得BH=AC,CD=DH,∠BHD=∠ACD,即可求得DG=DF,即可证明△CDF≌△HDG,可得∠GDH=∠CDF,根据∠CDF+∠ADF=90°即可解题.
解答:证明:∵∠ABC=45°,AD⊥BC,
∴BD=AD,
∵∠DBH+∠BHD=90°,∠AHE+∠CAD=90°,∠AHE=∠BHD,
∴∠DBH=∠CAD,
在△CAD和△HBD中,
,
∴△CAD≌△HBD(ASA),
∴BH=AC,CD=DH,∠BHD=∠ACD,
∵G为BH的中点,F为AC中点,
∴DG=
BH,DF=
AC,HG=CF,
∴DG=DF,
在△CDF和△HDG中,
,
∴△CDF≌△HDG(SAS),
∴∠GDH=∠CDF,
∵∠CDF+∠ADF=90°,
∴∠GDH+∠ADF=90°,即∠GDF=90°,
∴DG⊥DF.
∴BD=AD,
∵∠DBH+∠BHD=90°,∠AHE+∠CAD=90°,∠AHE=∠BHD,
∴∠DBH=∠CAD,
在△CAD和△HBD中,
|
∴△CAD≌△HBD(ASA),
∴BH=AC,CD=DH,∠BHD=∠ACD,
∵G为BH的中点,F为AC中点,
∴DG=
| 1 |
| 2 |
| 1 |
| 2 |
∴DG=DF,
在△CDF和△HDG中,
|
∴△CDF≌△HDG(SAS),
∴∠GDH=∠CDF,
∵∠CDF+∠ADF=90°,
∴∠GDH+∠ADF=90°,即∠GDF=90°,
∴DG⊥DF.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边、对应角相等的性质,本题中求证△CAD≌△HBD和△CDF≌△HDG是解题的关键.

练习册系列答案
相关题目
已知M(a,3)和N(4,b)关于y轴对称,则(a+b)2000的值为( )
| A、1 |
| B、-1 |
| C、72000 |
| D、-72000 |
 如图,△ABO与△DOC是否相似?为什么?
如图,△ABO与△DOC是否相似?为什么? 如图,在?ABCD中,对角线AC,BD相交于点O,若DO=1.5cm,AB=5cm,BC=4cm,求?ABCD的面积.
如图,在?ABCD中,对角线AC,BD相交于点O,若DO=1.5cm,AB=5cm,BC=4cm,求?ABCD的面积.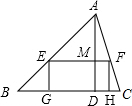 如图,矩形EFHG的边GH在△ABC边BC上,其他两个顶点分别在边AB、AC上,已知△ABC的边BC=120cm,BC边上的高AD为80cm;求:
如图,矩形EFHG的边GH在△ABC边BC上,其他两个顶点分别在边AB、AC上,已知△ABC的边BC=120cm,BC边上的高AD为80cm;求: