题目内容
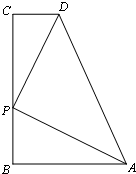 如图,已知四边形ABCD,∠B=∠C=90°,P是BC边上的一点,∠APD=90°.
如图,已知四边形ABCD,∠B=∠C=90°,P是BC边上的一点,∠APD=90°.(1)求证:△ABP∽△PCD;
(2)若BC=10,CD=3,PD=3
| 5 |
考点:相似三角形的判定与性质
专题:
分析:(1)证明∠BAP=∠CPD,∠B=∠C=90,即可解决问题.
(2)首先求出PC的长度;借助(1)中的△ABP∽△PCD,列出比例式即可解决问题.
(2)首先求出PC的长度;借助(1)中的△ABP∽△PCD,列出比例式即可解决问题.
解答: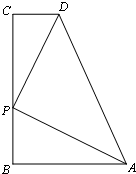 (1)证明:∵∠APD=90°,
(1)证明:∵∠APD=90°,
∠APB+∠APD+∠CPD=180°
∴∠APB+∠CPD=180°-∠APD=180°-900=900;
∵∠APB+∠BAP=90°,
∴∠BAP=∠CPD.
∵∠B=∠C=90°,
∴△ABP∽△PCD.
(2)解:由勾股定理得:
PC2=PD2-CD2=(3
)2-32,
∴PC=6,PB=10-6=4;
由(1)知,△ABP∽△PCD,
∴AB:PC=BP:CD,
∵BC=10,CD=3,PC=6,
∴AB:6=4:3,
∴AB=8.
 (1)证明:∵∠APD=90°,
(1)证明:∵∠APD=90°,∠APB+∠APD+∠CPD=180°
∴∠APB+∠CPD=180°-∠APD=180°-900=900;
∵∠APB+∠BAP=90°,
∴∠BAP=∠CPD.
∵∠B=∠C=90°,
∴△ABP∽△PCD.
(2)解:由勾股定理得:
PC2=PD2-CD2=(3
| 5 |
∴PC=6,PB=10-6=4;
由(1)知,△ABP∽△PCD,
∴AB:PC=BP:CD,
∵BC=10,CD=3,PC=6,
∴AB:6=4:3,
∴AB=8.
点评:该题主要考查了相似三角形的判定及其性质的应用问题;解题的关键是深入观察、大胆猜测、严格推理、科学论证.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知M(a,3)和N(4,b)关于y轴对称,则(a+b)2000的值为( )
| A、1 |
| B、-1 |
| C、72000 |
| D、-72000 |
 这是一根起点为0的数轴,现有同学将它弯折,如图所示,例如:第一行0,第二行6,第三行21…则虚线上的第10行的数是
这是一根起点为0的数轴,现有同学将它弯折,如图所示,例如:第一行0,第二行6,第三行21…则虚线上的第10行的数是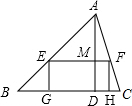 如图,矩形EFHG的边GH在△ABC边BC上,其他两个顶点分别在边AB、AC上,已知△ABC的边BC=120cm,BC边上的高AD为80cm;求:
如图,矩形EFHG的边GH在△ABC边BC上,其他两个顶点分别在边AB、AC上,已知△ABC的边BC=120cm,BC边上的高AD为80cm;求: 如图所示,已知△ADE∽△ABC,且AD=3,BD=CE=4,求AC的长.
如图所示,已知△ADE∽△ABC,且AD=3,BD=CE=4,求AC的长.