题目内容
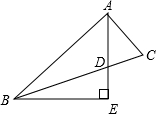 如图,AD是△ABC的角平分线,AD=AC,BE⊥AD于E
如图,AD是△ABC的角平分线,AD=AC,BE⊥AD于E(1)求证:AB-AC=2DE;
(2)求证:AB+AC=2AE.
考点:全等三角形的判定与性质,等腰三角形的判定与性质,三角形中位线定理
专题:证明题
分析:(1)延长AE至点F使得DE=EF,BD=BF,即可求得∠F=∠BDF=∠ADC=∠C,根据三角形内角和定理可求得∠ABF=∠C=∠F,可得AB=AF,即可解题;
(2)根据AE=AD+DE,AE=AF-EF和DE=DF即可求得2AE=AD+AF,再根据(1)中求得AB=AF即可解题.
(2)根据AE=AD+DE,AE=AF-EF和DE=DF即可求得2AE=AD+AF,再根据(1)中求得AB=AF即可解题.
解答:证明:(1)延长AE至点F使得DE=EF,
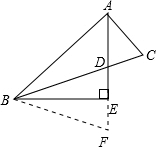
∵DE=EF,BE⊥DE,
∴BE垂直平分DF,
∴BD=BF,
∵AD=AC,
∴∠ADC=∠C,
∵∠ADC=∠BDC,
∴∠F=∠BDF=∠ADC=∠C,
∵AD是△ABC的角平分线,
∴∠BAD=∠CAD,
∵∠CAD+∠ADC+∠C=180°,∠BAD+∠F+∠ABF=180°,
∴∠ABF=∠C=∠F,
∴AB=AF,
∴AB-AC=AF-AD=DF=2DE;
(2)∵AE=AD+DE,AE=AF-EF,DE=EF,
∴2AE=AD+DE+AF-EF=AD+AF,
∵AF=AB,AC=AD,
∴2AE=AC+AB.

∵DE=EF,BE⊥DE,
∴BE垂直平分DF,
∴BD=BF,
∵AD=AC,
∴∠ADC=∠C,
∵∠ADC=∠BDC,
∴∠F=∠BDF=∠ADC=∠C,
∵AD是△ABC的角平分线,
∴∠BAD=∠CAD,
∵∠CAD+∠ADC+∠C=180°,∠BAD+∠F+∠ABF=180°,
∴∠ABF=∠C=∠F,
∴AB=AF,
∴AB-AC=AF-AD=DF=2DE;
(2)∵AE=AD+DE,AE=AF-EF,DE=EF,
∴2AE=AD+DE+AF-EF=AD+AF,
∵AF=AB,AC=AD,
∴2AE=AC+AB.
点评:本题考查了等腰三角形的判定和腰长相等的性质,考查了三角形内角和为180°的性质,本题中求得∠F=∠ABF是解题的关键.

练习册系列答案
相关题目
 已知点P为线段AB上一点,AP=
已知点P为线段AB上一点,AP= 利用二次函数y=
利用二次函数y= 这是一根起点为0的数轴,现有同学将它弯折,如图所示,例如:第一行0,第二行6,第三行21…则虚线上的第10行的数是
这是一根起点为0的数轴,现有同学将它弯折,如图所示,例如:第一行0,第二行6,第三行21…则虚线上的第10行的数是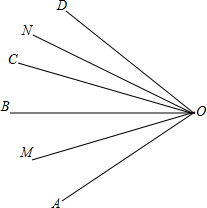 如图,OB、OC是∠AOD内的任意两条射线,OM平分∠AOB,ON平分∠COD,若∠MON=70°,∠BOC=30°,求∠AOD的度数.
如图,OB、OC是∠AOD内的任意两条射线,OM平分∠AOB,ON平分∠COD,若∠MON=70°,∠BOC=30°,求∠AOD的度数. 如图,△ABO与△DOC是否相似?为什么?
如图,△ABO与△DOC是否相似?为什么?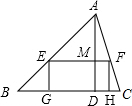 如图,矩形EFHG的边GH在△ABC边BC上,其他两个顶点分别在边AB、AC上,已知△ABC的边BC=120cm,BC边上的高AD为80cm;求:
如图,矩形EFHG的边GH在△ABC边BC上,其他两个顶点分别在边AB、AC上,已知△ABC的边BC=120cm,BC边上的高AD为80cm;求: