题目内容
13．若（2x+1）5=ax5+bx4+cx3+dx2+ex+f，求：（1）a+b+c+d+e+f的值，
（2）a-b+c-d+e-f的值，
（3）a和f的值．
分析 （1）令x=1求出所求式子的值即可；
（2）令x=-1求出所求式子的值即可；
（3）根据（1）与（2）求出a与f的值即可．
解答 解：（1）令x=1，得到a+b+c+d+e+f=243；
（2）令x=-1，得到a-b+c-d+e-f=-1；
（3）令x=0，得到f=1，a=32．
点评 此题考查了代数式求值，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
如图，一根电线杆AB直立于地面，拉线AC=6m，拉线底端C与电线杆底端B的距离为3m，求电线杆AB的高度．
8．某日孙老师佩戴运动手环进行快走锻炼，两次锻炼后数据如表．与第一次锻炼相比，孙老师第二次锻炼步数增长的百分率是其平均步长减少的百分率的3倍．根据经验已知孙老师第二次锻炼时平均步长减少的百分率小于0.5．
注：步数×平均步长=距离．
（1）求孙老师第二次锻炼时平均步长减少的百分率；
（2）孙老师发现好友中步数排名第一为24000步，因此在两次锻炼结束后又走了500米，使得总步数恰好为24000步，求孙老师这500米的平均步长．
| 项目 | 第一次锻炼 | 第二次锻炼 |
| 步数（步） | 10000 | ①10000（1+3x） |
| 平均步长（米/步） | 0.6 | ②0.6（1-x） |
| 距离（米） | 6000 | 7020 |
（1）求孙老师第二次锻炼时平均步长减少的百分率；
（2）孙老师发现好友中步数排名第一为24000步，因此在两次锻炼结束后又走了500米，使得总步数恰好为24000步，求孙老师这500米的平均步长．
18．下列根式中已经化简为最简形式的是（ ）
| A． | $\sqrt{8}$ | B． | $\sqrt{2{x}^{3}}$ | C． | $\sqrt{\frac{1}{3}}$ | D． | $\sqrt{{a}^{2}+{b}^{2}}$ |
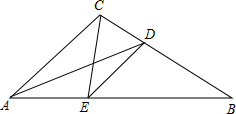如图，△ABC，∠BAC=40°，AD平分∠BAC，点E是AB上一点，连接CE、DE，∠ACE=40°，∠ADC=50°，求∠CED的度数．