题目内容
20.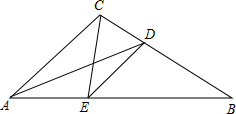 如图,△ABC,∠BAC=40°,AD平分∠BAC,点E是AB上一点,连接CE、DE,∠ACE=40°,∠ADC=50°,求∠CED的度数.
如图,△ABC,∠BAC=40°,AD平分∠BAC,点E是AB上一点,连接CE、DE,∠ACE=40°,∠ADC=50°,求∠CED的度数.
分析 作DF⊥AC,DG⊥CE,DH⊥AB,先根据角平分线的性质得到DG=DH,根据△EGD≌△EHD,得出∠CED=$\frac{1}{2}$∠CEB,就可以得到∠CED的度数.
解答 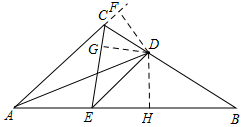 证明:作DF⊥AC,交AC的延长线于F,再作DG⊥CE,DH⊥AB,垂足分别为G,H,则
证明:作DF⊥AC,交AC的延长线于F,再作DG⊥CE,DH⊥AB,垂足分别为G,H,则
∵AD平分∠BAC,
∴DF=DH,
∵∠BAC=40°,AD平分∠BAC,
∴∠CAD=20°,
而∠ADC=50°,
∴∠FCD=20°+50°=70°,
又∵∠ACE=40°,
∴∠ECD=70°,
∴CD平分∠FCE,
∵DF⊥AC,DG⊥CE,
∴DF=DG,
∴DG=DH(等量代换),
又∵DE=DE,
∴Rt△EGA≌Rt△EPA(HL),
∴∠CED=$\frac{1}{2}$∠CEB=$\frac{1}{2}$(∠CAB+∠ACE)=$\frac{1}{2}$×80°=40°.
点评 本题主要考查三角形内角和定理、角平分线的性质定理及逆定理、三角形全等的性质和判定.掌握三角形内角和为180°,两次用到角平分线的知识是正确解答本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.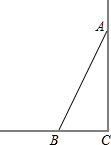 如图,一根长为5m的竹竿AB斜靠在竖直的墙壁上,竹竿底端B离墙壁距离3m,则该竹竿的顶端A离地竖直高度为( )
如图,一根长为5m的竹竿AB斜靠在竖直的墙壁上,竹竿底端B离墙壁距离3m,则该竹竿的顶端A离地竖直高度为( )
 如图,一根长为5m的竹竿AB斜靠在竖直的墙壁上,竹竿底端B离墙壁距离3m,则该竹竿的顶端A离地竖直高度为( )
如图,一根长为5m的竹竿AB斜靠在竖直的墙壁上,竹竿底端B离墙壁距离3m,则该竹竿的顶端A离地竖直高度为( )| A. | 2m | B. | 3m | C. | 4m | D. | $\sqrt{34}$m |