题目内容
1.若2(x+4)-5<3(x+1)+4的最小整数解是方程$\frac{1}{3}$x-mx=5的解,则m2-2m+11的平方根是$±\sqrt{11}$.分析 此题可先将不等式化简求出x的取值,然后取x的最小整数解代入方程2x-mx=4,化为关于m的一元一次方程,解方程即可得出m的值,进而就可求得m2-2m+11的平方根.
解答 解:由2(x+4)-5<3(x+1)+4得
x>-4,
所以最小整数解为x=-3,
将x=-3代入$\frac{1}{3}$x-mx=5中,
解得m=2.
则m2-2m+11=11,
11平方根为±$\sqrt{11}$
所以m2-2m+11的平方根是±$\sqrt{11}$,
故答案为±$\sqrt{11}$.
点评 此题主要考查了一元一次不等式的整数解,一元一次方程的解,以及代数式求值和平方根,关键是确定出x的值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.已知一次函数y=kx+3,当x=-1时,y=-1,那么当x=1时,y等于( )
| A. | 1 | B. | -1 | C. | 7 | D. | -7 |
 如图,在△ABC中,AD=AE,BD=EC,∠ADB=∠AEC,∠BAD=25°,则∠CAE的度数为25°.
如图,在△ABC中,AD=AE,BD=EC,∠ADB=∠AEC,∠BAD=25°,则∠CAE的度数为25°. 如图在平行四边形的纸片上有一个圆洞,请画一条直线把纸片分成分成面积相等的两部分.
如图在平行四边形的纸片上有一个圆洞,请画一条直线把纸片分成分成面积相等的两部分.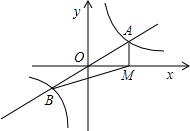 如图,直线y=mx与双曲线交y=$\frac{k}{x}$于A、B两点,过点A作AM⊥x轴,垂足为M,连结BM,若△ABM的面积等于2,则k的值是( )
如图,直线y=mx与双曲线交y=$\frac{k}{x}$于A、B两点,过点A作AM⊥x轴,垂足为M,连结BM,若△ABM的面积等于2,则k的值是( )