题目内容
9.解方程(1)$\frac{3}{x}$+$\frac{5}{2x-1}$=$\frac{x+27}{2{x}^{2}-x}$
(2)$\frac{x}{x-2}$+$\frac{2}{{x}^{2}-4}$=1.
分析 两分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:(1)去分母得:6x-3+5x=x+27,
解得:x=3,
经检验x=3是分式方程的解;
(2)去分母得:x2+2x+2=x2-4,
解得:x=-3,
经检验x=-3是分式方程的解.
点评 此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
4.若式子$\sqrt{-a-b}$+$\frac{1}{\sqrt{ab}}$有意义,则点P(a,b)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
18.若二次函数$y=m{x^2}+3x+\sqrt{3}$在平面直角坐标系中的图象与x轴有交点,则m的取值范围是( )
| A. | m>$\frac{{3\sqrt{3}}}{4}$ | B. | m≤$\frac{{3\sqrt{3}}}{4}$且m≠0 | C. | m>$\frac{{\sqrt{3}}}{4}$ | D. | m≤$\frac{{\sqrt{3}}}{4}$且m≠0 |
 如图,在△ABC中,AB=AC,点D在AC上,且在AB的垂直平分线上.若∠A=40°,则∠DBC=30°.
如图,在△ABC中,AB=AC,点D在AC上,且在AB的垂直平分线上.若∠A=40°,则∠DBC=30°.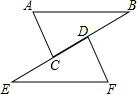 如图所示,AC=DF,BD=EC,AC∥DF,∠ACB=80°,∠B=30°,则∠F=70°.
如图所示,AC=DF,BD=EC,AC∥DF,∠ACB=80°,∠B=30°,则∠F=70°.