题目内容
已知一个半圆形工件,未搬动前如图,直径平行于地面放置,搬动时为了保护圆弧部分不受损伤,先将半圆作如图所示的无滑动翻转,使它的直径紧贴地面,再将它沿地面平移8米,半圆的直径为4米,则圆心O所经过的路线长是 米.


考点:弧长的计算
专题:
分析:根据题意得出球在无滑动旋转中通过的路程为
圆弧,后再平移8米,即可得出答案.
| 1 |
| 2 |
解答: 解:由图形可知,圆心先向前走OO1的长度即
解:由图形可知,圆心先向前走OO1的长度即
圆的周长,
然后沿着弧O1O2旋转
圆的周长,
然后后向右平移8米,
所以圆心总共走过的路程为圆周长的一半即半圆的弧长加上8米,
由已知得圆的半径为2米,
设半圆形的弧长为l,则半圆形的弧长l=
=2π(米),
故圆心O所经过的路线长=(8+2π)米.
故答案为:8+2π.
 解:由图形可知,圆心先向前走OO1的长度即
解:由图形可知,圆心先向前走OO1的长度即| 1 |
| 4 |
然后沿着弧O1O2旋转
| 1 |
| 4 |
然后后向右平移8米,
所以圆心总共走过的路程为圆周长的一半即半圆的弧长加上8米,
由已知得圆的半径为2米,
设半圆形的弧长为l,则半圆形的弧长l=
| (90+90)π×2 |
| 180 |
故圆心O所经过的路线长=(8+2π)米.
故答案为:8+2π.
点评:本题主要考查了弧长公式l=
,同时考查了平移的知识,解题关键是得出半圆形的弧长=半圆作无滑动翻转所经过的路线长.
| nπR |
| 180 |

练习册系列答案
相关题目
 彼此相似的矩形A1B1C1D1,A2B2C2D2,A3B3C3D3,…,按如图所示的方式放置.点A1,A2,A3,…,和点C1,C2,C3,…,分别在直线y=kx+b(k>0)和x轴上,已知点B1、B2的坐标分别为(1,2),(3,4),则Bn的坐标是( )
彼此相似的矩形A1B1C1D1,A2B2C2D2,A3B3C3D3,…,按如图所示的方式放置.点A1,A2,A3,…,和点C1,C2,C3,…,分别在直线y=kx+b(k>0)和x轴上,已知点B1、B2的坐标分别为(1,2),(3,4),则Bn的坐标是( )| A、(2n-1,2n) | ||
B、(2n-
| ||
C、(2n-1-
| ||
| D、(2n-1-1,2n-1) |
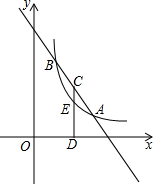 如图,一次函数y1=-x+4的图象与反比例函数y2=
如图,一次函数y1=-x+4的图象与反比例函数y2= 如图,M为双曲线y=
如图,M为双曲线y= 如图是甲、乙两射击运动员的10次射击训练成绩(环数)的折线统计图,观察图形,甲、乙这10次射击成绩的方差S甲2,S乙2之间的大小关系是
如图是甲、乙两射击运动员的10次射击训练成绩(环数)的折线统计图,观察图形,甲、乙这10次射击成绩的方差S甲2,S乙2之间的大小关系是 如图,圆柱形容器中,高为120cm,底面周长为100cm,在容器内壁离容器底部40cm的点B处有一蚊子,此时一只壁虎正好在容器外壁,离容器上沿40cm与蚊子相对的点A处,则壁虎捕捉蚊子的最短距离为
如图,圆柱形容器中,高为120cm,底面周长为100cm,在容器内壁离容器底部40cm的点B处有一蚊子,此时一只壁虎正好在容器外壁,离容器上沿40cm与蚊子相对的点A处,则壁虎捕捉蚊子的最短距离为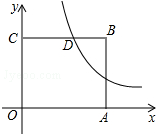 如图,在平面直角坐标系中,正方形OABC的边OA、OC分别在x轴、y轴上,点B的坐标为(4,4),反比例函数的图象经过CB的中点D,若点P(x,y)在该反比例函数的图象上运动(不与点D重合),过点P作PR⊥y轴于点R,作PQ⊥BC所在直线于点Q,记四边形CQPR的面积为S=4时,x的值为
如图,在平面直角坐标系中,正方形OABC的边OA、OC分别在x轴、y轴上,点B的坐标为(4,4),反比例函数的图象经过CB的中点D,若点P(x,y)在该反比例函数的图象上运动(不与点D重合),过点P作PR⊥y轴于点R,作PQ⊥BC所在直线于点Q,记四边形CQPR的面积为S=4时,x的值为