题目内容
8. 如图,直线y=-3x+3与x轴交于点A,与y轴交于点C,点B为x轴正半轴上一点,∠ACB=45°,求点B的坐标(多种方法).
如图,直线y=-3x+3与x轴交于点A,与y轴交于点C,点B为x轴正半轴上一点,∠ACB=45°,求点B的坐标(多种方法).
分析 方法一,如图1中作PA⊥AC使得PA=AC,延长AP与x轴交于点B,PE⊥AB于E,由△AOC≌△PEA,得AE=CO=3,PE=OA=1,所以点P坐标(4,1),求出直线PC即可解决问题.
方法二,如图2中作BP⊥CA交CA的延长线于P,PE⊥OB于E,PQ⊥CO于Q,由△PCQ≌△PBE,得PQ=PE,可以求得点P坐标($\frac{3}{2}$,-$\frac{3}{2}$),求出直线PB即可解决问题.
解答 解:方法一,如图1中, 作PA⊥AC使得PA=AC,延长AP与x轴交于点B,PE⊥AB于E.
作PA⊥AC使得PA=AC,延长AP与x轴交于点B,PE⊥AB于E.
∵∠CAP=∠AEP=∠AOC=90°,
∴∠ACO+∠OAC=90°,∠OAC+∠PAE=90°,
∴∠ACO=∠PAE,
在△AOC和△PEA中,
$\left\{\begin{array}{l}{∠ACO=∠PAE}\\{∠COA=∠PEA}\\{AC=AP}\end{array}\right.$,
∴△AOC≌△PEA,
∴AE=CO=3,PE=OA=1,
∴点P坐标(4,1),
∴直线PC为y=-$\frac{1}{2}$x+3,
∴点B坐标(6,0).
方法二,如图2中, 作BP⊥CA交CA的延长线于P,PE⊥OB于E,PQ⊥CO于Q.
作BP⊥CA交CA的延长线于P,PE⊥OB于E,PQ⊥CO于Q.
∵∠ACO+∠OAC=90°,∠PBE+∠PAB=90°,∠OAC=∠PAB,
∴∠ACO=∠PBE,
∵∠PCB=45°,∠CPB=90°,
∴∠PCB=∠PBC=45°,
∴PC=PB,
在△PCQ和△PBE中,
$\left\{\begin{array}{l}{∠PCQ=∠PBE}\\{∠PQC=∠PEB}\\{PC=PB}\end{array}\right.$,
∴△PCQ≌△PBE,
∴PQ=PE,
∵点P在直线AC上,
∴点P坐标($\frac{3}{2}$,-$\frac{3}{2}$),
∴直线PB为y=$\frac{1}{3}x-2$,
∴点B坐标为(6,0).
点评 本题考查全等三角形的判定和性质、等腰直角三角形的判定和性质、一次函数的应用,解决问题的关键是添加辅助线构造全等三角形,利用一次函数解决问题,体现了转化的思想,属于中考常考题型.

 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 如图,平行四边形ABCD中,BM=4,且AM=5,BD=12,AD=9,则ABCD的面积是$\frac{540}{13}$.
如图,平行四边形ABCD中,BM=4,且AM=5,BD=12,AD=9,则ABCD的面积是$\frac{540}{13}$.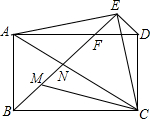 如图,矩形ABCD中,AB=3,AD=4,△ACE为等腰直角三角形,∠AEC=90°,连接BE交AD、AC分别于F、N,CM平分∠ACB交BN于M,则MN:NF=5:9.
如图,矩形ABCD中,AB=3,AD=4,△ACE为等腰直角三角形,∠AEC=90°,连接BE交AD、AC分别于F、N,CM平分∠ACB交BN于M,则MN:NF=5:9.