题目内容
7. 如图,在每个小正方形的边长为1的网格中,点A,B均在格点上,即AB=4,
如图,在每个小正方形的边长为1的网格中,点A,B均在格点上,即AB=4,点E为线段AB上的动点.若使得BE=$\frac{16}{9}$,则$\frac{AE}{BE}$的值为$\frac{5}{4}$;请你在网格中,用无刻度的直尺,找到点E的位置,并简要说明此位置是如何找到的(不要求证明)在B所在横线的上边第9条线上找到格点F,连接BF,BF交F下距离是5的横线与BF的交点是G,过G作GE∥AF交AB于点E,点E就是所求..
分析 首先求得AE的长,即可求得$\frac{AE}{BE}$的值,根据平行线分线段成比例定理即可作出E的位置.
解答 解:AE=AB-BE=4-$\frac{16}{9}$=$\frac{20}{9}$,
则$\frac{AE}{BE}$=$\frac{\frac{20}{9}}{\frac{16}{9}}$=$\frac{20}{16}$=$\frac{5}{4}$.
找到E的方法:在B所在横线的上边第9条线上找到格点F,连接BF,BF交F下距离是5的横线与BF的交点是G,过G作GE∥AF交AB于点E,点E就是所求.
点评 本题考查了线段的比值,以及平行线分线段成比例定理,正确理解利用平行线分线段成比例定理是关键.

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
2.下列结论中正确的是( )
| A. | 0既是正数,又是负数 | B. | 0既不是正数,也不是负数 | ||
| C. | 0是最小的正数 | D. | 0是最大的负数 |
4.下列关于全等三角形的说法,其中正确的是( )
| A. | 周长相等的两个等边三角形全等 | B. | 斜边相等的两个直角三角形全等 | ||
| C. | 面积相等的两个三角形全等 | D. | 腰长相等的两个等腰三角形全等 |
 如图,已知正方形OABC的边长为2,顶点A,C分别在x轴,y轴的正半轴上,E点是BC的中点,F是AB延长线上一点且FB=1.
如图,已知正方形OABC的边长为2,顶点A,C分别在x轴,y轴的正半轴上,E点是BC的中点,F是AB延长线上一点且FB=1. 如图,O是直线AB上一点,已知∠AOC=50°,OD平分∠AOC.
如图,O是直线AB上一点,已知∠AOC=50°,OD平分∠AOC. 如图,已知AD=CB,AE=CF,DE=BF,求证:DE∥BF.
如图,已知AD=CB,AE=CF,DE=BF,求证:DE∥BF.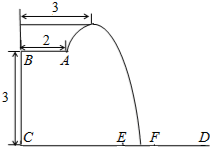 在2014年仁川亚运会上中国队包揽了跳水所有项目的金牌.过去十一届亚运会的跳水金牌也全部归于中国跳水队!优秀成绩的取得离不开艰辛的训练.某跳水运动员在进行一次跳水训练时,身体(看成一点)在空中的运动路线是如图所示的一条抛物线.已知跳板AB长为2米,跳板距水面CD高BC为3米,为安全和空中姿势优美,训练时跳水曲线在离起跳点水平距离1米时达到距水面最大高度4米,现以CD为横轴,CB为纵轴建立直角坐标系.
在2014年仁川亚运会上中国队包揽了跳水所有项目的金牌.过去十一届亚运会的跳水金牌也全部归于中国跳水队!优秀成绩的取得离不开艰辛的训练.某跳水运动员在进行一次跳水训练时,身体(看成一点)在空中的运动路线是如图所示的一条抛物线.已知跳板AB长为2米,跳板距水面CD高BC为3米,为安全和空中姿势优美,训练时跳水曲线在离起跳点水平距离1米时达到距水面最大高度4米,现以CD为横轴,CB为纵轴建立直角坐标系.