题目内容
5.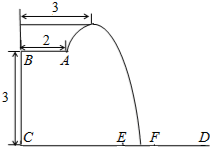 在2014年仁川亚运会上中国队包揽了跳水所有项目的金牌.过去十一届亚运会的跳水金牌也全部归于中国跳水队!优秀成绩的取得离不开艰辛的训练.某跳水运动员在进行一次跳水训练时,身体(看成一点)在空中的运动路线是如图所示的一条抛物线.已知跳板AB长为2米,跳板距水面CD高BC为3米,为安全和空中姿势优美,训练时跳水曲线在离起跳点水平距离1米时达到距水面最大高度4米,现以CD为横轴,CB为纵轴建立直角坐标系.
在2014年仁川亚运会上中国队包揽了跳水所有项目的金牌.过去十一届亚运会的跳水金牌也全部归于中国跳水队!优秀成绩的取得离不开艰辛的训练.某跳水运动员在进行一次跳水训练时,身体(看成一点)在空中的运动路线是如图所示的一条抛物线.已知跳板AB长为2米,跳板距水面CD高BC为3米,为安全和空中姿势优美,训练时跳水曲线在离起跳点水平距离1米时达到距水面最大高度4米,现以CD为横轴,CB为纵轴建立直角坐标系.(1)求这条抛物线的解析式;
(2)图中CE=4.5米,CF=5.5米,若跳水运动员在区域EF内入水时才能达到训练要求,试通过计算说明这次跳水是否能达到要求.
分析 (1)根据题意建立平面直角坐标系,进而利用顶点式求出抛物线解析式;
(2)利用y=0时,求出图象与x轴交点,进而得出答案.
解答  解:(1)如图所示:可得抛物线顶点坐标M(3,4),A(2,3)
解:(1)如图所示:可得抛物线顶点坐标M(3,4),A(2,3)
设抛物线解析为:y=a(x-3)2+4,
则3=a(2-3)2+4,
解得:a=-1,
故抛物线解析式为:y=-(x-3)2+4;
(2)由题意可得:当y=0,则0=-(x-3)2+4,
解得:x1=1,x2=5,
故抛物线与x轴交点为:(5,0),
则这次跳水能达到要求.
点评 此题主要考查了二次函数的应用,根据题意利用顶点式求出二次函数解析式是解题关键.

练习册系列答案
相关题目
20.在一幅比例尺为1:500000的地图上,若量得甲、乙两地的距离是25cm,则甲、乙两地实际距离为( )
| A. | 125km | B. | 12.5km | C. | 1.25km | D. | 1250km |
 如图,在每个小正方形的边长为1的网格中,点A,B均在格点上,即AB=4,
如图,在每个小正方形的边长为1的网格中,点A,B均在格点上,即AB=4, 如图所示,在△ABC中,∠A=90°,∠ABC的平分线与∠ACB的平分线相交于点O,求∠BOC的度数.
如图所示,在△ABC中,∠A=90°,∠ABC的平分线与∠ACB的平分线相交于点O,求∠BOC的度数. 如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$图象交于A,B两点,与x轴交于点C(-2,0),点A的横坐标为1,S△AOC=2.
如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$图象交于A,B两点,与x轴交于点C(-2,0),点A的横坐标为1,S△AOC=2. 如图,在矩形ABCD中,AB=3,BC=4,点E在BC边上运动,连结AE,过点D作DF⊥AE,垂足为F,设AE=x,DF=y,则能反映y与x之间函数关系的大致图象是( )
如图,在矩形ABCD中,AB=3,BC=4,点E在BC边上运动,连结AE,过点D作DF⊥AE,垂足为F,设AE=x,DF=y,则能反映y与x之间函数关系的大致图象是( )



