题目内容
14.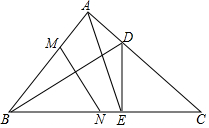 如图,△ABC中,∠BAC=90°,AB=AC,D为AC上一点,DE⊥BC于E,连接BD,M在AB上,AM=AD,MN⊥BD交BC于点N,若MN=5,AE=5$\sqrt{2}$,求BC的长.
如图,△ABC中,∠BAC=90°,AB=AC,D为AC上一点,DE⊥BC于E,连接BD,M在AB上,AM=AD,MN⊥BD交BC于点N,若MN=5,AE=5$\sqrt{2}$,求BC的长.
分析 连接AN,作MK⊥BC于K,连接DM、EM.只要证明△MBN∽△EBA,可得$\frac{BM}{AE}$=$\frac{BN}{AB}$=$\frac{MN}{AE}$=$\frac{5}{5\sqrt{2}}$=$\frac{\sqrt{2}}{2}$,推出AB=$\sqrt{2}$BN,由∠ABC=45°,推出BN=NC,AN⊥BC,由$\frac{BN}{BM}$=$\frac{AB}{AE}$,∠ABN=∠EBM,推出△ABN∽△EBM,推出∠MEB=∠BAN=45°,推出MK=KE=DE=DM=EC=KB,KN=NE,设EN=a,则AN=NC=3a,在Rt△ANE中,可得a2+9a2=50,求出a即可解决问题.
解答 解:连接AN,作MK⊥BC于K,连接DM、EM.
∵∠BAD+∠BED=180°,
∴A、B、E、D四点共圆,
∴∠EBD=∠EAD,
∵∠EBD+∠BNM=90°,∠DAE+∠BAE=90°,
∴∠BNM=∠BAE,∵∠MBN=∠ABE,
∴△MBN∽△EBA,
∴$\frac{BM}{AE}$=$\frac{BN}{AB}$=$\frac{MN}{AE}$=$\frac{5}{5\sqrt{2}}$=$\frac{\sqrt{2}}{2}$,
∴AB=$\sqrt{2}$BN,
∵∠ABC=45°,
∴BN=NC,AN⊥BC,
∵$\frac{BN}{BM}$=$\frac{AB}{AE}$,∠ABN=∠EBM,
∴△ABN∽△EBM,
∴∠MEB=∠BAN=45°,
∴MK=KE=DE=DM=EC=KB,KN=NE,设EN=a,则AN=NC=3a,
在Rt△ANE中,a2+9a2=50,
∵a>0,
∴a=$\sqrt{5}$,
∴BC=6a=6$\sqrt{5}$.
点评 本题考查全等三角形的判定和性质、等腰直角三角形的性质、勾股定理.相似三角形的判定和性质,解得的突破点是证明点N是BC的中点,四边形DMKE是正方形,题目比较难,用到四点共圆.

 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案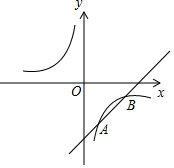 如图,已知一次函数y=kx+b与反比例函数y=$\frac{m}{x}$交于A(1,-3),B(a,-1)两点.
如图,已知一次函数y=kx+b与反比例函数y=$\frac{m}{x}$交于A(1,-3),B(a,-1)两点.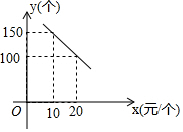 某旅游风景区出售一种纪念品,该纪念品的成本为12元/个,这种纪念品的销售价格为x(元/个)与每天的销售数量y(个)之间的函数关系如图所示.
某旅游风景区出售一种纪念品,该纪念品的成本为12元/个,这种纪念品的销售价格为x(元/个)与每天的销售数量y(个)之间的函数关系如图所示. 某商场为了吸引顾客,设立了一个可以自由转动的转盘(如图,转盘被平均分成20份),并规定:顾客每购物满200元,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得50元、30元、20元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转盘,那么可直接获得10元的购物券.
某商场为了吸引顾客,设立了一个可以自由转动的转盘(如图,转盘被平均分成20份),并规定:顾客每购物满200元,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得50元、30元、20元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转盘,那么可直接获得10元的购物券.