题目内容
4．计算：（$\frac{1}{2}$）-1+4cos 60°-|-3|+$\sqrt{9}$-（-2017）0+（-1）2016．分析 原式利用零指数幂、负整数指数幂法则，特殊角的三角函数值，绝对值的代数意义，算术平方根定义，以及乘方的意义计算即可得到结果．
解答 解：原式=2+2-3+3-1+1=4．
点评 此题考查了实数的运算，零指数幂、负整数指数幂，以及特殊角的三角函数值，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
14．
有这样一个问题：探究函数y=$\frac{1}{2}$（x-1）（x-2）（x-3）+x的性质．
（1）先从简单情况开始探究：
①当函数y=$\frac{1}{2}$（x-1）+x时，y随x增大而增大（填“增大”或“减小”）；
②当函数y=$\frac{1}{2}$（x-1）（x-2）+x时，它的图象与直线y=x的交点坐标为（1，1），（2，2）；
（2）当函数y=$\frac{1}{2}$（x-1）（x-2）（x-3）+x时，
下表为其y与x的几组对应值．
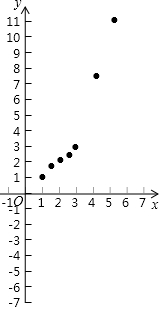
①如图，在平面直角坐标系xOy中，描出了上表中各对对应值为坐标的点，请根据描出的点，画出该函数的图象；
②根据画出的函数图象，写出该函数的一条性质：y随x的增大而增大．
有这样一个问题：探究函数y=$\frac{1}{2}$（x-1）（x-2）（x-3）+x的性质．（1）先从简单情况开始探究：
①当函数y=$\frac{1}{2}$（x-1）+x时，y随x增大而增大（填“增大”或“减小”）；
②当函数y=$\frac{1}{2}$（x-1）（x-2）+x时，它的图象与直线y=x的交点坐标为（1，1），（2，2）；
（2）当函数y=$\frac{1}{2}$（x-1）（x-2）（x-3）+x时，
下表为其y与x的几组对应值．
| x | … | -$\frac{1}{2}$ | 0 | 1 | $\frac{3}{2}$ | 2 | $\frac{5}{2}$ | 3 | 4 | $\frac{9}{2}$ | … |
| y | … | -$\frac{113}{16}$ | -3 | 1 | $\frac{27}{16}$ | 2 | $\frac{37}{16}$ | 3 | 7 | $\frac{177}{16}$ | … |
②根据画出的函数图象，写出该函数的一条性质：y随x的增大而增大．
15．下列方程中，是二元一次方程的是（ ）
| A． | xy=1 | B． | x-$\frac{2}{y}$=3 | C． | x-y=1 | D． | x2-y+3=0 |
12．下列命题中，真命题是（ ）
| A． | 对角线相等的四边形是矩形 | |
| B． | 对角线互相垂直的四边形是菱形 | |
| C． | 两条对角线互相平分且相等的四边形是正方形 | |
| D． | 顺次连接四边形的各边中点所得的四边形是平行四边形 |
19．对于等式：（1）（-am）n=（-an）m；（2）[（-a）m]n=[（-a）n]m．判断正确的是（ ）
| A． | （1）正确 | B． | （2）正确 | C． | 都正确 | D． | 无法判断 |
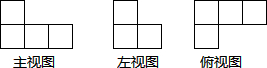在一个仓库里堆放有若干个相同的正方体货箱，仓库管理员将这堆货箱的三视图画出来，如图，则这堆货箱共有5个．
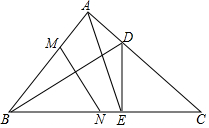如图，△ABC中，∠BAC=90°，AB=AC，D为AC上一点，DE⊥BC于E，连接BD，M在AB上，AM=AD，MN⊥BD交BC于点N，若MN=5，AE=5$\sqrt{2}$，求BC的长．