题目内容
15.等边三角形的外接圆半径为4cm,求此三角形的面积.分析 连接OA、OB,作OD⊥BC于D,根据正三角形中心角的计算公式求出∠BOD的度数,根据勾股定理求出OD、BC,根据三角形面积公式求出答案.
解答 解: O为△ABC的外心,连接OA、OB,作OD⊥BC于D,
O为△ABC的外心,连接OA、OB,作OD⊥BC于D,
∵∠BOD=360°÷3÷2=60°,OB=4,
∴OD=2,BD=2$\sqrt{3}$,
则BC=4$\sqrt{3}$,
∴△ABC的面积=$\frac{1}{2}$×4$\sqrt{3}$×2×3=12$\sqrt{3}$.
点评 本题考查的是三角形的外接圆和外心的知识,掌握三角形的外心的概念、中心角的求法和三角形的半径的概念是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
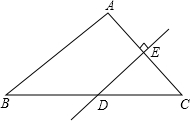 如图,△ABC的周长为24,AC的垂直平分线交BC于点D,E为垂足.若AE=4,求△ABD的周长.
如图,△ABC的周长为24,AC的垂直平分线交BC于点D,E为垂足.若AE=4,求△ABD的周长.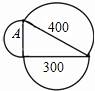 如图,半圆内数字分别为所在半圆的面积,则图中字母A所代表的半圆面积是100.
如图,半圆内数字分别为所在半圆的面积,则图中字母A所代表的半圆面积是100.