题目内容
9．圆内接四边形相邻三个内角之比是3：4：6，则该四边形内角中最大度数是120°．分析 设三个内角为3x，4x，6x，根据圆内接四边形的对角互补列出方程，解方程求出x，计算出各角的度数，比较得到答案．
解答 解：设三个内角为3x，4x，6x，
根据圆内接四边形的对角互补，得
3x+6x=180°，
∴x=20°
则这三个内角为60°、80°、120°，
所以第四个内角是180°-4x=100°，
所以该四边形内角中最大度数是120°，
故答案为：120°．
点评 本题考查的是圆内接四边形的性质，掌握圆内接四边形的对角互补是解题的关键．
练习册系列答案
相关题目
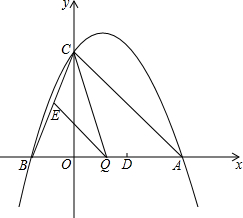如图，在平面直角坐标系中，已知抛物线经过A（4，0），B（-2，0），C（0，4）三点．
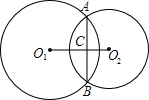已知：如图，⊙O1与⊙O2相交于A、B，若两圆半径分别为17cm和10cm，公共弦AB=16cm，求O1O2的长．
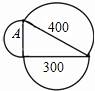如图，半圆内数字分别为所在半圆的面积，则图中字母A所代表的半圆面积是100．
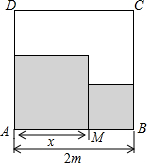如图，在边长为2m的正方形铁板内，沿着一条边恰好截取两块相邻的正方形板料，要使截取的板料面积最小，应该怎样截取？