题目内容

19．⊙O中，M为$\widehat{AB}$的中点，则下列结论正确的是（　　）
A．∠AOB＞2∠AOMB．∠AOB=2∠AOM
C．∠AOB＜2∠AOMD．∠AOB与2∠AOM的大小不能确定

分析 根据题意先画出图形，再根据在同圆或等圆中，同弧或等弧所对的圆周角相等，即可得出正确的结论．

解答 解：根据题意如图：
∵在⊙O中，M为$\widehat{AB}$的中点，
∴$\widehat{AM}$=$\widehat{MB}$，
∴∠AOM=∠MOB，
∴∠AOB=2∠AOM；
故选B．

点评 此题考查了圆心角、弧、弦之间的关系，掌握在同圆或等圆中，同弧或等弧所对的圆周角相等是本题的关键．

练习册系列答案
相关题目
9．为拉动内需促进消费，某品牌的电视机经过两次降价，从原来每台6000元降到现在的每台4860元，求平均每次的降价率是多少？设每次降价率为x，由题意列方程为（　　）
A．4860（1+x）2=6000B．4860（1-x）2=6000C．6000（1-x）2=4860D．6000（1+x）2=4860
10．下列判断不正确的是（　　）
A．$\overrightarrow a-\overrightarrow a=\overrightarrow 0$B．如果$|{\overrightarrow a}|=|{\overrightarrow b}|$，那么$\overrightarrow a=\overrightarrow b$
C．如果$\overrightarrow a=k•\overrightarrow b$（k≠0），那么$\overrightarrow a∥\overrightarrow b$D．$\overrightarrow a+\overrightarrow b=\overrightarrow b+\overrightarrow a$
7．给出下列命题：
①在直角三角形ABC中，已知两边长为3和4，则第三边长为5；
②三角形的三边a、b、c满足a2+c2=b2，则∠C=90°；
③△ABC中，若∠A：∠B：∠C=1：5：6，则△ABC是直角三角形；
④△ABC中，若三边长分别为3a、4a、5a（a＞0），则这个三角形是直角三角形．
其中，假命题的个数为（　　）
A．1个B．2个C．3个D．4个
14．解为x=-3的方程是（　　）
A．2x-6=0B．3（x-2）-2（x-3）=5xC．$\frac{3x+3}{2}$=6D．$\frac{x-1}{4}$=$\frac{3-2x}{6}$-$\frac{5}{2}$
5．小明有5张卡片写着不同的数字的卡片，请你分别按要求抽出卡片，

写出符合要求的算式：
（1）从中取出2张卡片，使这2张卡片上数字乘积最大；
（2）从中取出2张卡片，使这2张卡片上数字相除的商最小；
（3）从中取出2张卡片，用学过的运算方法，使这2张卡片上数字组成一个最大的数；
（4）从中取出4张卡片，用学过的运算方法，使结果为24．（写出一种即可）
12．用计算器计算：（结果保留两位小数）
（1）（-37）×125÷（-75）；
（2）-4.375×（-0.112）-2.321÷（-5.157）．
9．等边三角形ABC中，点D、E分别在BC、AB上，连接AD、CE交于点F，作CG⊥AD于点G，AE=BD．
（1）如图1，当DC=2BD时，求证：F是AG的中点；
（2）如图2，过点A作AH⊥CE的延长线于H，连接HG并延长，交BC于点N，当HN⊥BC时，求证：AH=$\sqrt{2}$GN．
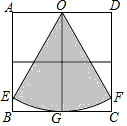10．如图，四个小正方形的边长都是1，若以O为圆心，OG为半径作弧分别交AB、DC于点E、F，则图中阴影部分的面积为$\frac{2π}{3}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网