Question

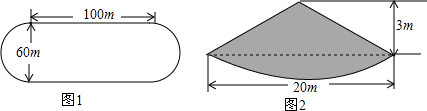
9．甲场地如图1所示，中间长为100m，宽为60m的长方形，两边为两个半圆，现欲在甲场地上铺一层厚4cm的煤，乙地为一售煤点，该售煤点有一堆煤近似一个圆锥，如图2所示，该圆锥底面圆的直径为20m，高为6m．
（1）甲场地需用的煤为多少立方米？乙地售煤点的这堆煤是否够用？说明理由．（π取3.14）
（2）甲地有A型货车及B型货车，A型车每辆可载煤15立方米，每辆B型车的载煤体积是每辆A型车载煤体积的$\frac{4}{3}$倍，现甲地有A型货车10辆去乙地运煤，至少还需几辆B型货车，才能将甲地所需的煤一次从乙地运回．（结果保留整数）
（3）A型车和B型车匀速行驶在甲乙两地，A型车与B型车的速度比为4：3，一辆B型车从甲地出发1小时后一辆A型车从甲地出发，沿B型车所行进的路线去乙地，B型货车到达乙地后装煤用去13分钟，然后原路返回与前来乙地的A型车相遇，此时这辆A型车出发21分钟，该A型车此时所行驶的路程比甲乙两地路程的一半多4千米，求甲乙两地的路程．

Answer 1

分析 （1）先求得如图1和图2所示场地中煤的体积，然后比较大小即可判断；
（2）先求得一辆B型车的载重体积，然后根据A型车的载重煤的体积+B型车的载重煤的体积=乙地煤的总体积列方程求解即可；
（3）A型车的速度为每分钟4xkm，B型车的速度为每分钟3xkm．根据A型车此时所行驶的路程比甲乙两地路程的一半多4km列方程求解即可．

解答 解：（1）甲场地的面积S=3.14×30²+100×60=8826m²．
则甲场地需要煤的总体积=8826×0.04=353.04m³．
乙地有煤的体积=$\frac{1}{3}$×3.14×10²×6=628m³．
∵353.04＜628，
∴乙地的煤够用．
（2）一辆B型车的载重体积=15×$\frac{4}{3}$=20m³．
设需要B型车x辆，根据题意得；10×15+20x=628．
解得：x=23.9．
答：至少需要B型车24辆．
（3）设A型的速度为每分钟4y千米，B型的速度为每分钟3y千米．
根据题意得；4y×21=$\frac{1}{2}$×$\frac{1}{2}$×（68×3y+21×4y）+4．
解得；y=$\frac{1}{3}$．
甲乙两地的路程为（4×21×$\frac{1}{3}$-4）×2=48．
答：甲乙两地的路程为48千米．

点评 本题主要考查的是一元一次方程的应用，用含y的式子表示出甲乙两地之间的距离是解题的关键．