题目内容
4.在y=$\frac{3x-6}{-x+1}$中,当x取何值时,(1)y是正数?
(2)y是负数?
(3)y的值是0?
分析 (1)根据y是正数,得到$\left\{\begin{array}{l}{3x-6>0}\\{-x+1>0}\end{array}\right.$或$\left\{\begin{array}{l}{3x-6<0}\\{-x+1<0}\end{array}\right.$,即可解答;
(2)根据y是负数,得到$\left\{\begin{array}{l}{3x-6>0}\\{-x+1<0}\end{array}\right.$或$\left\{\begin{array}{l}{3x+6<0}\\{-x+1>0}\end{array}\right.$,即可解答;
(3)根据y的值是0,即3x-6=0,且-x+1≠0,即可解答.
解答 解:(1)∵y是正数,
∴$\left\{\begin{array}{l}{3x-6>0}\\{-x+1>0}\end{array}\right.$或$\left\{\begin{array}{l}{3x-6<0}\\{-x+1<0}\end{array}\right.$,
解得:1<x<2.
(2)∵y是负数,
∴$\left\{\begin{array}{l}{3x-6>0}\\{-x+1<0}\end{array}\right.$或$\left\{\begin{array}{l}{3x+6<0}\\{-x+1>0}\end{array}\right.$,
解得:x>2或x<-2.
(3)∵y的值是0,
∴3x-6=0,且-x+1≠0,
解得:x=2.
点评 本题考查分式的值,解决本题的关键是明确分式的值为0,为分式的分子为0,且分母不等于0.

练习册系列答案
相关题目
13.高度每增加1千米,气温大约下降6℃,现在地面气温是10℃,那么高度增加3千米后,高空的气温是( )
| A. | -8℃ | B. | -18℃ | C. | -28℃ | D. | 18℃ |
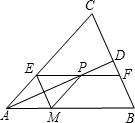 已知等腰△ABC中,AB=AC,AD平分∠BAC交BC于D点,在线段AD上任取一点P(A点除外),过P点作EF∥AB,分别交AC,BC于E,F点,作PM∥AC,交AB于M点,连接ME.
已知等腰△ABC中,AB=AC,AD平分∠BAC交BC于D点,在线段AD上任取一点P(A点除外),过P点作EF∥AB,分别交AC,BC于E,F点,作PM∥AC,交AB于M点,连接ME.
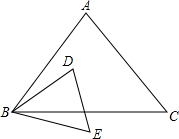 如图,在△ABC和△DBE中,$\frac{AB}{BD}$=$\frac{BC}{BE}$=$\frac{AC}{DE}$=$\frac{3}{2}$.
如图,在△ABC和△DBE中,$\frac{AB}{BD}$=$\frac{BC}{BE}$=$\frac{AC}{DE}$=$\frac{3}{2}$.