题目内容
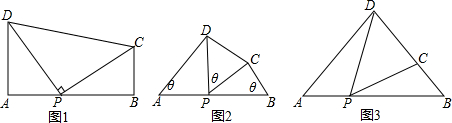
16.请同学们仔细阅读以下内容:数学课上,老师向同学们介绍了直角三角形的性质:直角三角形斜边上的中线等于斜边的一半.
如图1,在Rt△ABC中,∠ACB=90°,点D是边AB的中点,则CD=AD=BD=$\frac{1}{2}$AB.
请同学们借助以上知识点探究下面问题:
如图2,Rt△ABC≌Rt△EDF,∠ACB=∠F=90°,∠A=∠E=30°.△EDF绕着边AB的中点D旋转,DE,DF分别交线段AC于点M,K.
(1)观察:①如图3、图4,当∠CDF=0°或60°时,AM+CK=MK(填“>”,“<”或“=”).
②如图5,当∠CDF=30° 时,AM+CK>MK(只填“>”或“<”).
(2)猜想:如图1,当0°<∠CDF<60°时,若点G是点A关于直线DE的对称点,则AM+CK>MK,证明你所得到的结论.
(3)如果MK2+CK2=AM2,请直接写出∠CDF的度数.
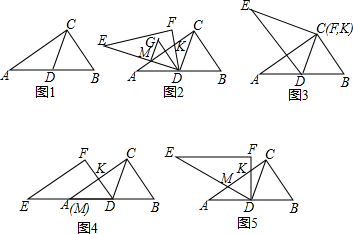
分析 (1)先证明△CDA是等腰三角形,再根据等腰三角形的性质证明AM+CK=MK;在△MKD中,AM+CK>MK(两边之和大于第三边);
(2)作点C关于FD的对称点G,连接GK,GM,GD.证明△ADM≌△GDM后,根据全等三角形的性质可得GM=AM,GM+GK>MK,从而得到AM+CK>MK;
(3)根据勾股定理的逆定理求得∠GKM=90°,又由点C关于FD的对称点G,得到∠CKG=90°,∠FKC=$\frac{1}{2}$∠CKG=45°,根据三角形的外角定理,就可以求得∠CDF=15°.
解答 解:(1)①在Rt△ABC中,D是AB的中点,
∴AD=BD=CD=$\frac{1}{2}$AB,∠B=∠BDC=60°
又∵∠A=30°,
∴∠ACD=60°-30°=30°,
又∵∠CDE=60°,或∠CDF=60°时,
∴∠CKD=90°,
∴在△CDA中,AM(K)=CM(K),即AM(K)=KM(C)(等腰三角形底边上的垂线与中线重合),
∵CK=0,或AM=0,
∴AM+CK=MK;
②由①,得
∠ACD=30°,∠CDB=60°,
又∵∠A=30°,∠CDF=30°,∠EDF=60°,
∴∠ADM=30°,
∴AM=MD,CK=KD,
∴AM+CK=MD+KD,
∴在△MKD中,AM+CK>MK(两边之和大于第三边),
故答案为:①=;②>;
(2)>,
证明:连接GK,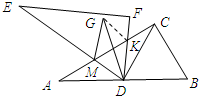
∵点G是点A关于直线DE的对称点
∴AD=GD,GM=AM,∠GDM=∠ADM,
∵Rt△ABC 中,D是AB的中点,
∴AD=CD=GD.
∵∠A=∠E=30°,
∴∠CDA=120°,∠EDF=60°,
∴∠GDM+∠GDK=60°,∠ADM+∠CDK=60°,
∴∠GDK=∠CDK,
在△GDK和△CDK中,
$\left\{\begin{array}{l}GD=CD\\∠GDK=∠CDK\\ DK=DK\end{array}\right.$,
∴△GDK≌△CDK,
∴GK=CK,
∵GM+GK>MK,
∴AM+CK>MK;
(3)∠CDF=15°,
由(2),得GM=AM,GK=CK,
∵MK2+CK2=AM2,
∴MK2+GK2=GM2,
∴∠GKM=90°,
又∵点C关于FD的对称点G,
∴∠CKG=90°,∠FKC=$\frac{1}{2}$∠CKG=45°,
又∵由(1),得∠A=∠ACD=30°,
∴∠FKC=∠CDF+∠ACD,
∴∠CDF=∠FKC-∠ACD=15°.
点评 本题综合考查了全等三角形的判定、全等三角形的性质、轴对称图形的性质以及三角形的两边之和大于第三边的性质.

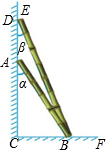 如图,有两根竹竿AB、DB靠在墙角上,并与墙角FCE形成一定的角度,测得∠CAB,∠CDB的度数分别为α,β.用含有α,β的代数式表示∠DBF和∠ABD的度数.
如图,有两根竹竿AB、DB靠在墙角上,并与墙角FCE形成一定的角度,测得∠CAB,∠CDB的度数分别为α,β.用含有α,β的代数式表示∠DBF和∠ABD的度数.