题目内容
4.探究与应用(1)问题
如图1,在四边形ABCD中,点P为AB上一点,AD=BP,∠A=∠B=∠DPC=90°,求证:△ADP≌△BPC.
(2)探究
如图2,在四边形ABCD中,点P为AB上一点,AD=BP,∠A=∠B=∠DPC=θ时,上述结论是否依然成立?说明理由.
(3)应用请利用(1)(2)获得的经验解决问题:
图3,在△ABD中,AB=6,AD=BD=BP=5,且满足∠A=∠DPC,求DC的长.
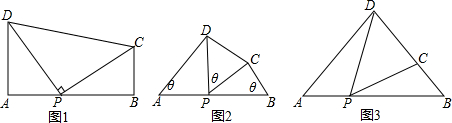
分析 (1)如图1,由∠DPC=∠A=∠B=90°可得∠ADP=∠BPC,即可证到△ADP≌△BPC;
(2)如图2,由∠DPC=∠A=∠B=θ可得∠ADP=∠BPC,即可证到△ADP∽△BPC,然后运用相似三角形的性质即可解决问题;
(3)如图3,过点D作DE⊥AB于点E,根据等腰三角形的性质可得AE=BE=3,根据勾股定理可得DE=4,由题可得DC=DE=4.
解答 解:(1)∵∠DPC=∠A=∠B=90°,
∴∠ADP+∠APD=90°,
∠BPC+∠APD=90°,
∴∠ADP=∠BPC,
在△ADP与△BPC中,
$\left\{\begin{array}{l}{∠A=∠B}\\{∠ADP=∠BPC}\\{AD=PB}\end{array}\right.$,
∴△ADP≌△BPC;
(2)结论AD•BC=AP•BP仍然成立.理由:
∵∠BPD=∠DPC+∠BPC,∠BPD=∠A+∠ADP,
∴∠DPC+∠BPC=∠A+∠ADP.
∵∠DPC=∠A=∠B=θ,
∴∠BPC=∠ADP,
∴△ADP∽△BPC,
∴$\frac{AD}{BP}=\frac{AP}{BC}$,
∴AD•BC=AP•BP;
(3)过点D作DE⊥AB于点E.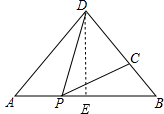
∵AD=BD=5,AB=6,
∴AE=BE=3.
由勾股定理可得DE=4.
∴DC=DE=4.
点评 本题考查了全等三角形的判定与性质,关键是根据由∠DPC=∠A=∠B=90°可得∠ADP=∠BPC,即可证到△ADP≌△BPC.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
15.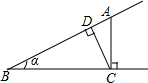 如图,点A为∠α边上任意一点,作AC⊥BC于点C,CD⊥AB于点D,下列用线段比表示sinα的值,错误的是( )
如图,点A为∠α边上任意一点,作AC⊥BC于点C,CD⊥AB于点D,下列用线段比表示sinα的值,错误的是( )
 如图,点A为∠α边上任意一点,作AC⊥BC于点C,CD⊥AB于点D,下列用线段比表示sinα的值,错误的是( )
如图,点A为∠α边上任意一点,作AC⊥BC于点C,CD⊥AB于点D,下列用线段比表示sinα的值,错误的是( )| A. | $\frac{CD}{BC}$ | B. | $\frac{AC}{AB}$ | C. | $\frac{AD}{AC}$ | D. | $\frac{CD}{AC}$ |
12.若-2a2b4与5an-2b2m是同类项,则mn的值是( )
| A. | 2 | B. | 4 | C. | 8 | D. | 16 |
 已知:二次函数y=ax2+bx+c的图象如图所示,下列结论中:
已知:二次函数y=ax2+bx+c的图象如图所示,下列结论中: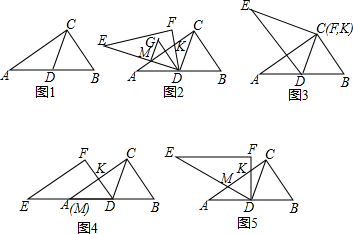
 如图,坐标系中正方形网格的单位长度为1,抛物线y1=-$\frac{1}{2}{x^2}$+3向下平移2个单位后得抛物线y2,则阴影部分的面积S=4.
如图,坐标系中正方形网格的单位长度为1,抛物线y1=-$\frac{1}{2}{x^2}$+3向下平移2个单位后得抛物线y2,则阴影部分的面积S=4.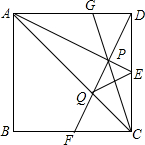 如图,正方形ABCD中,E、F分别为CD、BC的中点,AE、DF交于点P.
如图,正方形ABCD中,E、F分别为CD、BC的中点,AE、DF交于点P.