题目内容
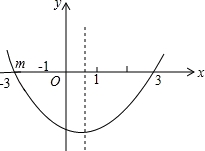
如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,现有下列结论:①abc<0;②b2﹣4ac+5>0;③2a+b<0;④a﹣b+c<0;⑤抛物线y=ax2+bx+c(a≠0)与x轴的另一个点坐标为(﹣1,0),其中正确的是__________(把所有正确结论的序号都填在横线上)
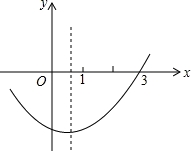
②④
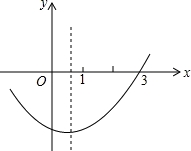
【考点】二次函数图象与系数的关系.
【专题】推理填空题;数形结合.
【分析】由抛物线的开口方向可确定a的符号,由抛物线的对称轴相对于y轴的位置可得a与b之间的符号关系,由抛物线与y轴的交点位置可确定c的符号;由抛物线与x轴交点个数可确定b2﹣4ac的符号;根据抛物线的对称轴与x=1的大小关系可推出2a+b的符号;根据抛物线的对称性即可知道抛物线与x轴的左交点位置;由于x=﹣1时y=a﹣b+c,因而结合图象,可根据x=﹣1时y的符号来确定a﹣b+c的符号.
【解答】解:由抛物线的开口向上可得a>0,
由抛物线的对称轴在y轴的右边可得x=﹣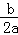 >0,则a与b异号,因而b<0,
>0,则a与b异号,因而b<0,
由抛物线与y轴的交点在y轴的负半轴上可得c<0,
∴abc>0,故①错误;
由抛物线与x轴有两个交点可得b2﹣4ac>0,因而b2﹣4ac+5>0,故②正确;
由抛物线的对称轴x=﹣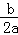 <1(a>0),可得﹣b<2a,即2a+b>0,故③错误;
<1(a>0),可得﹣b<2a,即2a+b>0,故③错误;
设抛物线与x轴的左交点为(m,0),根据对称性可得:
抛物线的对称轴x=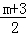 .
.
由图可知0<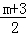 <1,
<1,
解得﹣3<m<﹣1.
因而抛物线与x轴的另一个交点坐标不是(﹣1,0),故⑤错误;
当x=﹣1时y<0,即a﹣b+c<0,故④正确;
综上所述:②、④正确.
故答案为②、④.
【点评】本题主要考查二次函数图象与系数的关系,其中a决定于抛物线的开口方向,b决定于抛物线的开口方向及抛物线的对称轴相对于y轴的位置,c决定于抛物线与y轴的交点位置,b2﹣4ac的符号决定于抛物线与x轴交点个数,2a+b的符号决定于a的符号及﹣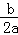 与1的大小关系,运用数形结合的思想准确获取相关信息是解决本题的关键.
与1的大小关系,运用数形结合的思想准确获取相关信息是解决本题的关键.

 阅读快车系列答案
阅读快车系列答案 +
+ =0的根( )
=0的根( ) ,x2=-
,x2=- 的变形中,是因式分解的是( )
的变形中,是因式分解的是( ) ,BD=
,BD= ,则AB的长为( )
,则AB的长为( )
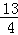 ,y1),B(
,y1),B(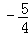 ,y2),C(
,y2),C(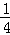 ,y3)为二次函数y=x2+4x﹣5的图象上的三点,则y1,y2,y3的大小关系是( )
,y3)为二次函数y=x2+4x﹣5的图象上的三点,则y1,y2,y3的大小关系是( )