题目内容
2. 如图,△ABC中,∠A=90°,∠C=75°,AC=6,DE垂直平分BC,则BE的值为( )
如图,△ABC中,∠A=90°,∠C=75°,AC=6,DE垂直平分BC,则BE的值为( )| A. | 12 | B. | 6$\sqrt{3}$ | C. | 8 | D. | 9 |
分析 根据三角形的内角和求出∠B=15°,再根据垂直平分线的性质求出BE=EC,∠1=∠B=15°,然后解直角三角形计算.
解答  解:如图,连接EC.
解:如图,连接EC.
∵△ABC中,∠A=90°,∠C=75°,
∴∠B=15°.
∵DE垂直平分BC,
∴BE=EC,∠1=∠B=15°
∴∠2=∠ACB-∠1=75°-15°=60°
在Rt△ACE中,∠2=60°,∠A=90°
∴∠3=180°-∠2-∠A=180°-60°-90°=30°
故EC=2AC=2×6=12,
即BE=12.
故选A.
点评 本题主要考查线段的垂直平分线的性质及含30°角的直角三角形的性质等几何知识;求得∠3=30°是正确解答本题的关键.

练习册系列答案
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
17.【分校】下面三个有理数$-\frac{3}{4}$,$-\frac{5}{6}$,$-\frac{7}{8}$的大小顺序是( )
| A. | $-\frac{7}{8}$$<-\frac{5}{6}$$<-\frac{3}{4}$ | B. | $-\frac{7}{8}$$<-\frac{3}{4}$$<-\frac{5}{6}$ | C. | $-\frac{5}{6}$$<-\frac{7}{8}$$<-\frac{3}{4}$ | D. | $-\frac{3}{4}$$<-\frac{5}{6}$$<-\frac{7}{8}$ |
 如图,二次函数y=ax2+bx+c的最大值为$\frac{13}{6}$,其图象经过点A(0,-2)、B(5,-2),点C在x轴上,∠ACB=90°,且CA<CB,将△ABC饶点A逆时针旋转,使点C的对应点C′落在x轴上.
如图,二次函数y=ax2+bx+c的最大值为$\frac{13}{6}$,其图象经过点A(0,-2)、B(5,-2),点C在x轴上,∠ACB=90°,且CA<CB,将△ABC饶点A逆时针旋转,使点C的对应点C′落在x轴上.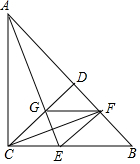 如图.在Rr△ABC中,∠ACB=90°,CD⊥AB于D,∠BAC的平分线交CD于G,交BC于E,∠DCB的平分线交BD于F,连接EF,FG.
如图.在Rr△ABC中,∠ACB=90°,CD⊥AB于D,∠BAC的平分线交CD于G,交BC于E,∠DCB的平分线交BD于F,连接EF,FG. 如图,在△ABC中,∠C=90°,∠BAC=60°,∠BAC的平分线交BC于D,若AD=6cm,则BC=9 cm.
如图,在△ABC中,∠C=90°,∠BAC=60°,∠BAC的平分线交BC于D,若AD=6cm,则BC=9 cm.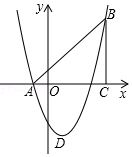 如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90,AC=BC,OA=1,OC=4,抛物线y=x2+bx+c经过A,B两点,抛物线的顶点为D.
如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90,AC=BC,OA=1,OC=4,抛物线y=x2+bx+c经过A,B两点,抛物线的顶点为D. 如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.
如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.