题目内容
7.计算:(1)(a2+3a)÷$\frac{{a}^{2}-9}{3-a}$;
(2)(a+$\frac{1}{a+2}$)÷(a-2+$\frac{3}{a+2}$).
分析 (1)因式分解,把除法改为乘法计算即可;
(2)先通分计算括号里面的加法,再算除法.
解答 解:(1)原式=a(a+3)•$\frac{3-a}{(a+3)(a-3)}$
=-a;
(2)原式=$\frac{{a}^{2}+2a+1}{a+2}$÷$\frac{{a}^{2}-4+3}{a+2}$
=$\frac{(a+1)^{2}}{a+2}$•$\frac{a+2}{(a+1)(a-1)}$
=$\frac{a+1}{a-1}$.
点评 此题考查分式的混合运算,掌握运算顺序与运算方法是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.下列图形既是轴对称图形又是中心对称图形的是( )
| A. | 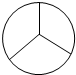 | B. | 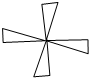 | C. | 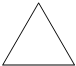 | D. |  |
12.要使二次根式$\sqrt{5-2x}$有意义,则x的取值范围是( )
| A. | x$>\frac{5}{2}$ | B. | x$≥\frac{2}{5}$ | C. | x$≤\frac{5}{2}$ | D. | x$≤\frac{2}{5}$ |
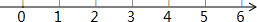 解不等式组$\left\{\begin{array}{l}{x+3≥4①}\\{3x-4≤11②}\end{array}\right.$
解不等式组$\left\{\begin{array}{l}{x+3≥4①}\\{3x-4≤11②}\end{array}\right.$ 如图是4×4的正方形网格,请选取一个白色的正方形并涂上阴影,使图中阴影部分是一个中心对称图形.
如图是4×4的正方形网格,请选取一个白色的正方形并涂上阴影,使图中阴影部分是一个中心对称图形.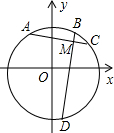 半径为2的圆的圆心O在直角坐标系的原点,两条互相垂直的弦AC和BD相交于点M(1,$\sqrt{2}$),则四边形ABCD的面积的最大值与最小值的差是1.
半径为2的圆的圆心O在直角坐标系的原点,两条互相垂直的弦AC和BD相交于点M(1,$\sqrt{2}$),则四边形ABCD的面积的最大值与最小值的差是1.