题目内容
17.甲、乙两人对代数式$\frac{x-y}{\sqrt{x}-\sqrt{y}}$分别进行不同方式的变形:甲:$\frac{x-y}{\sqrt{x}-\sqrt{y}}$=$\frac{(x-y)}{(\sqrt{x}-\sqrt{y})}$•$\frac{(\sqrt{x}+\sqrt{y})}{(\sqrt{x}+\sqrt{y})}$=$\frac{(x-y)(\sqrt{x}+\sqrt{y})}{x-y}$=$\sqrt{x}+\sqrt{y}$
乙:$\frac{x-y}{\sqrt{x}-\sqrt{y}}$=$\frac{(\sqrt{x}+\sqrt{y})(\sqrt{x}-\sqrt{y})}{\sqrt{x}-\sqrt{y}}$=$\sqrt{x}+\sqrt{y}$
(1)这两种变形方法是否正确?为什么?
(2)若对代数式$\frac{x-y}{\sqrt{x}+\sqrt{y}}$化简,能否采用上述方法?若能,请你试一试;若不能,请说明理由.
分析 (1)利用分母有理化对甲进行判断;利用因式分解的方法对乙进行判断;
(2)由于$\sqrt{x}$-$\sqrt{y}$可能为0,则可利用乙的方法计算$\frac{x-y}{\sqrt{x}+\sqrt{y}}$.
解答 解:(1)甲、乙的方法都正确.对于甲,把分子分母都乘以($\sqrt{x}$+$\sqrt{y}$),再约分得到结果;对于乙,利用平方差公式把分子分解,然后约分即可;
(2)对代数式$\frac{x-y}{\sqrt{x}+\sqrt{y}}$化简可采用乙的方法.
$\frac{x-y}{\sqrt{x}+\sqrt{y}}$=$\frac{(\sqrt{x}+\sqrt{y})(\sqrt{x}-\sqrt{y})}{\sqrt{x}+\sqrt{y}}$=$\sqrt{x}$-$\sqrt{y}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
相关题目
2.若$\frac{a}{b}$=$\frac{c}{d}$=$\frac{1}{2}$,(b-2d≠0),则$\frac{a-2c}{b-2d}$=( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | -$\frac{1}{4}$ |
9.若△ABC中,AB=25cm,AC=26cm,BC边上的高AD=24cm,则BC的长为( )
| A. | 17cm | B. | 3cm | C. | 17cm或3cm | D. | 以上都不对 |
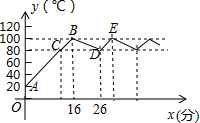 张老师办公室的饮水机具有自动调节功能,开机后自动进行加热状态,水温y(℃)与开机后用时x(分钟)成一次函数关系,当水温上升到100℃时停止加热,水温开始下降,此时水温y(℃)与开机后用时x(分钟)仍成一次函数某天早晨7:00时,张老师打开饮水机,水温变化情况如图所示.
张老师办公室的饮水机具有自动调节功能,开机后自动进行加热状态,水温y(℃)与开机后用时x(分钟)成一次函数关系,当水温上升到100℃时停止加热,水温开始下降,此时水温y(℃)与开机后用时x(分钟)仍成一次函数某天早晨7:00时,张老师打开饮水机,水温变化情况如图所示.