题目内容
4.如图,在直角坐标系中,四边形OABC为直角梯形,A点的坐标为(2,0),C点的坐标为(1,$\sqrt{3}$)(1)B点坐标为(2,$\sqrt{3}$),∠COA的度数为60度.
(2)边长为1的正方形ODEF的顶点F,D分别在x,y轴上,现将正方形沿着线段OC,CB翻滚(无滑动)请在备用图中画出翻滚过程中顶点E的运动痕迹,并求出运动的路程.

分析 (1)过点C作CM⊥OA,根据A和C点的坐标可直接得出B点的坐标;根据C点的坐标求出OM和CM的值,再根据勾股定理求出OC,从而得出∠COA的度数;
(2)顶点E的运动痕迹有2段:①以OE长为半径,圆心角为30°的弧长;②以DE长为半径,圆心角为45°的弧长;把两者的长度相加即可求解.
解答  解:(1)如图,过点C作CM⊥OA,
解:(1)如图,过点C作CM⊥OA,
∵A点的坐标为(2,0),C点的坐标为(1,$\sqrt{3}$)
∴B点坐标为(2,$\sqrt{3}$),
∴OM=1,CM=$\sqrt{3}$,
∴OC=2,
∴sin∠COA=$\frac{MC}{OC}$=$\frac{\sqrt{3}}{2}$,
∴∠COA=60°; (2)如备用图:
(2)如备用图:
①以OE长为半径,圆心角为30°的弧长,
在Rt△ODE中,OE=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,
90°-60°=30°,
$\frac{30×π×\sqrt{2}}{180}$=$\frac{\sqrt{2}π}{6}$;
②以DE长为半径,圆心角为45°的弧长,
$\frac{45×π×1}{180}$=$\frac{π}{4}$;
运动的路程为$\frac{\sqrt{2}π}{6}$+$\frac{π}{4}$=($\frac{\sqrt{2}}{6}$+$\frac{1}{4}$)π.
故答案为:(2,$\sqrt{3}$),60.
点评 此题考查了作图-旋转变换,用到的知识点是勾股定理、特殊角的三角函数值和旋转的性质,关键是根据题意画出图形.

练习册系列答案
相关题目
11.2014年,历下的教育惠民政策引起了社会的广泛关注,其中包括投入3600万元,免费为区属义务教育阶段中小学生提供校服.3600万元用科学记数表示为( )
| A. | 36×107元 | B. | 36×106元 | C. | 3.6×107元 | D. | 3.6×106元 |
 如图,△ABC和△DCE都是边长为2的等边三角形,点B、C、E在同一条直线上,连接BD,求BD的长.
如图,△ABC和△DCE都是边长为2的等边三角形,点B、C、E在同一条直线上,连接BD,求BD的长.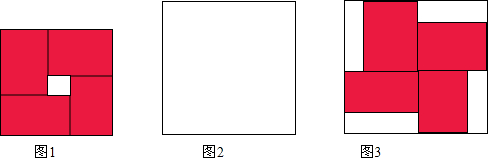
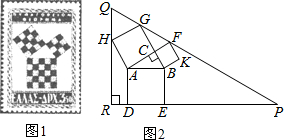 勾股定理有着悠久的历史,它曾引起很多人的兴趣.l955年希腊发行了二枚以勾股图为背景的邮票图1所示.所谓勾股图是指以直角三角形的三边为边向外作正方形构成,它可以验证勾股定理.在如图2的勾股图中,已知∠ACB=90°,∠BAC=30°,AB=4.作△PQR使得∠R=90°,点H在边QR上,点D,E在边PR上,点G,F在边PQ上,则RQ=7+2$\sqrt{3}$,△PQR的周长等于27+13$\sqrt{3}$.
勾股定理有着悠久的历史,它曾引起很多人的兴趣.l955年希腊发行了二枚以勾股图为背景的邮票图1所示.所谓勾股图是指以直角三角形的三边为边向外作正方形构成,它可以验证勾股定理.在如图2的勾股图中,已知∠ACB=90°,∠BAC=30°,AB=4.作△PQR使得∠R=90°,点H在边QR上,点D,E在边PR上,点G,F在边PQ上,则RQ=7+2$\sqrt{3}$,△PQR的周长等于27+13$\sqrt{3}$.