题目内容
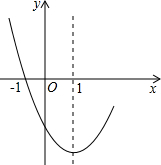若二次函数y=x2-2x+c的部分图象如图所示，则关于x的方程x2-2x+c=0的两根为考点：抛物线与x轴的交点
专题：
分析：由图象可知二次函数过（-1，0），代入可求得c的值，再令y=0可求得方程的两根．
解答：解：
∵二次函数过点（-1，0），
∴0=1+2+c，解得c=-3，
∴二次函数解析式为y=x2-2x-3，
令y=0可得0=x2-2x-3，解得x=-1或3，
即方程x2-2x+c=0的两根为-1或3，
故答案为：-1或3．
∵二次函数过点（-1，0），
∴0=1+2+c，解得c=-3，
∴二次函数解析式为y=x2-2x-3，
令y=0可得0=x2-2x-3，解得x=-1或3，
即方程x2-2x+c=0的两根为-1或3，
故答案为：-1或3．
点评：本题主要考查二次函数图象与x轴的交点与一元二次方程的根的关系，由条件求得c的值是解题的关键，注意方程的根是函数图象与x轴交点的横坐标．
练习册系列答案
相关题目
直角三角板ABC中，∠A=30°，BC=1，将其绕直角顶点C逆时针旋转一个角α（0°＜α＜90°），得到Rt△A′B′C，在三角板旋转的过程中，边A′C与AB交于点D，过点D作DE∥A′B′交 C B′，边于点E，连接BE．国家决定对某药品价格分两次降价，若设平均每次降价的百分比为x，该药品的原价为36元，降价后的价格为y元，则y与x之间的函数关系为（ ）
| A、y=72（1-x） |
| B、y=36（1-x） |
| C、y=36（1-x2） |
| D、y=36（1-x）2 |
已知二次函数y=-x2+2x-3a的部分图象如图所示，则关于x的一元二次方程-x2+2x-3a=0的解为
如图，抛物线y=x2-4x+3与x轴交于A、B两点，与y轴正半轴交于点C．在此抛物线上是否存在一点P，使直线OP与抛物线只有点P这个公共点？若存在请求出点P的坐标；若不存在，请说明理由．下列说法：①角是轴对称图形，对称轴是角的平分线；②等腰三角形至少有1条对称轴，至多有3条对称轴；③关于某直线对称的两个三角形一定是全等三角形；④两图形关于某直线对称，对称点一定在直线的两旁，其中正确的有（ ）
| A、4个 | B、3个 | C、2个 | D、1个 |
如图，△ABC是等边三角形，D为AC的中点，DE⊥AB，垂足为E．则图中和△AED相似的三角形（不包含△AED）有（ ）| A、1个 | B、2个 | C、3个 | D、4个 |