题目内容
 已知二次函数y=-x2+2x-3a的部分图象如图所示,则关于x的一元二次方程-x2+2x-3a=0的解为
已知二次函数y=-x2+2x-3a的部分图象如图所示,则关于x的一元二次方程-x2+2x-3a=0的解为考点:抛物线与x轴的交点
专题:
分析:由图象可知二次函数过(3,0),代入可求得a的值,再令y=0可求得方程的两根.
解答:解:∵二次函数过点(3,0),
∴0=-9+6-3a,解得a=-1,
∴二次函数解析式为y=-x2+2x+3,
令y=0可得0=-x2+2x+3,解得x1=3,x2=-1,
即方程-x2+2x-3a=0的两根为x1=3,x2=-1,
故答案为:x1=3,x2=-1.
∴0=-9+6-3a,解得a=-1,
∴二次函数解析式为y=-x2+2x+3,
令y=0可得0=-x2+2x+3,解得x1=3,x2=-1,
即方程-x2+2x-3a=0的两根为x1=3,x2=-1,
故答案为:x1=3,x2=-1.
点评:本题主要考查二次函数图象与x轴的交点与一元二次方程的根的关系,由条件求得a的值是解题的关键,注意方程的根是函数图象与x轴交点的横坐标.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
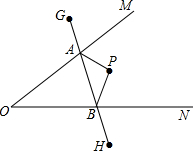 如图,∠MON内有一点P,P点关于OM的轴对称点是G,P点关于ON的轴对称点是H,GH分别交OM、ON于A、B点.若GH的长为10cm,求△PAB的周长为( )
如图,∠MON内有一点P,P点关于OM的轴对称点是G,P点关于ON的轴对称点是H,GH分别交OM、ON于A、B点.若GH的长为10cm,求△PAB的周长为( )| A、5cm | B、10cm |
| C、20cm | D、15cm |
已知方程组
的解满足x+2y≤a,则( )
|
| A、a≥3 | ||
| B、a≤3 | ||
C、a≥
| ||
D、a≤-
|
 把长方体的八个角切去一个角后,余下的图形有
把长方体的八个角切去一个角后,余下的图形有 如图,?ABCD中,点E,F分别为边AD,BC上的点,且AE=CF,AF,BE交于点G,CE,DF交于点H.试问:EF和GH是否互相平分?为什么?
如图,?ABCD中,点E,F分别为边AD,BC上的点,且AE=CF,AF,BE交于点G,CE,DF交于点H.试问:EF和GH是否互相平分?为什么? 如图,抛物线y=-x2+4ax-3经过点M(2,1),交x轴于A、B,交y轴负半轴于C.平移CM交x轴于D,交对称轴右边的抛物线于P,使
如图,抛物线y=-x2+4ax-3经过点M(2,1),交x轴于A、B,交y轴负半轴于C.平移CM交x轴于D,交对称轴右边的抛物线于P,使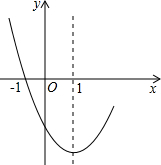 若二次函数y=x2-2x+c的部分图象如图所示,则关于x的方程x2-2x+c=0的两根为
若二次函数y=x2-2x+c的部分图象如图所示,则关于x的方程x2-2x+c=0的两根为