题目内容
如图，△ABC是等边三角形，D为AC的中点，DE⊥AB，垂足为E．则图中和△AED相似的三角形（不包含△AED）有（ ）| A、1个 | B、2个 | C、3个 | D、4个 |
考点：相似三角形的判定
专题：
分析：利用等边三角形的性质得出各角的度数，进而得出和△AED相似的三角形．
解答：解：∵△ABC是等边三角形，D为AC的中点，DE⊥AB，垂足为E，
∴∠ABD=∠CBD=30°，∠A=∠C=60°，
∴∠ADE=30°，
则图中和△AED相似的三角形（不包含△AED）有：△ADB，△DEB，△CDB．
故选：C．
∴∠ABD=∠CBD=30°，∠A=∠C=60°，
∴∠ADE=30°，
则图中和△AED相似的三角形（不包含△AED）有：△ADB，△DEB，△CDB．
故选：C．
点评：此题主要考查了相似三角形的判定以及等边三角形的性质，得出三角形各内角度数是解题关键．
练习册系列答案
发散思维新课堂系列答案
相关题目
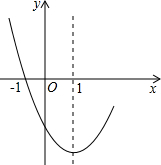若二次函数y=x2-2x+c的部分图象如图所示，则关于x的方程x2-2x+c=0的两根为已知方程组
的解满足x+2y≤a，则（ ）
|
| A、a≥3 | ||
| B、a≤3 | ||
C、a≥
| ||
D、a≤-
|
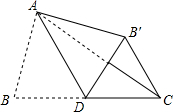如图，在△ABC中，BC=5，AD为BC边上的中线，∠ADB=60°，将△ABD沿线段AD翻折，点B翻折到点B′的位置，连接CB′，则CB′的长为（ ）