题目内容
 直角三角板ABC中,∠A=30°,BC=1,将其绕直角顶点C逆时针旋转一个角α(0°<α<90°),得到Rt△A′B′C,在三角板旋转的过程中,边A′C与AB交于点D,过点D作DE∥A′B′交 C B′,边于点E,连接BE.
直角三角板ABC中,∠A=30°,BC=1,将其绕直角顶点C逆时针旋转一个角α(0°<α<90°),得到Rt△A′B′C,在三角板旋转的过程中,边A′C与AB交于点D,过点D作DE∥A′B′交 C B′,边于点E,连接BE.(1)求证:△CAD∽△CBE;
(2)设AD=x,BE=y,求y与x之间的函数解析式;
(3)当S△BDE′=
| 1 |
| 5 |
考点:相似形综合题
专题:
分析:(1)根据平行线分线段成比例得出
=
,再由旋转的性质可知,CA=CA',CB=CB',∠ACD=∠BCE,由此得出△CAD∽△CBE;
(2)根据相似三角形的对应边成比例、直角三角形的性质及∠A=30°求得y=
x(0<x<2);
(3)先根据三角形的面积公式先求出△ABC的面积,再由△CAD∽△CBE,求得BE,分情况讨论:当点D在AB边上时,AD=x,BD=AB-AD=2-x;当点D在AB的延长线上时,AD=x,BD=x-2,再根据S△BDE=
BD×BE,代入相应的值求出x的值,即可得出答案.
| CD |
| CA′ |
| CE |
| CB′ |
(2)根据相似三角形的对应边成比例、直角三角形的性质及∠A=30°求得y=
| ||
| 3 |
(3)先根据三角形的面积公式先求出△ABC的面积,再由△CAD∽△CBE,求得BE,分情况讨论:当点D在AB边上时,AD=x,BD=AB-AD=2-x;当点D在AB的延长线上时,AD=x,BD=x-2,再根据S△BDE=
| 1 |
| 2 |
解答:解:(1)当0°<α<90°时,点D在AB边上(如图),
∵DE∥A'B',
∴
=
,
由旋转性质可知,CA=CA',CB=CB',∠ACD=∠BCE.
∴
=
,
∴
=
,
∴△CAD∽△CBE.
(2)∵△CAD∽△CBE,
∴
=
.
∵∠A=30°,
∴
=
=
,
∴y=
x(0<x<2);
(3)当0°<α<90°时,点D在AB边上,
AD=x,BD=AB-AD=2-x,∠DBE=90°.
此时,S=S△BDE=
BD×BE=
(x-2)×
=
.
当S=
S△ABC时,
=
.
整理,得x2-2x+1=0.
解得x1=x2=1,即AD=1.
当90°<α<120°时,点D在AB的延长线线上(如图),
设AD=x,则BD=x-2,∠DBE=90°.
S=S△BDE=
BD×BE=
(x-2)×
=
.
当S═
S△ABC时,
=
.
整理,得x2-2x-1=0.
解得 x1=1+
,x2=1-
(负值,舍去).
即AD=1+
.
综上所述:AD=1或AD=1+
.
∵DE∥A'B',
∴
| CD |
| CA′ |
| CE |
| CB′ |
由旋转性质可知,CA=CA',CB=CB',∠ACD=∠BCE.
∴
| CD |
| CA |
| CE |
| CB |
∴
| CD |
| CE |
| CA |
| CB |
∴△CAD∽△CBE.
(2)∵△CAD∽△CBE,
∴
| BE |
| AD |
| BC |
| AC |
∵∠A=30°,
∴
| y |
| x |
| BC |
| AC |
| ||
| 3 |
∴y=
| ||
| 3 |
(3)当0°<α<90°时,点D在AB边上,
AD=x,BD=AB-AD=2-x,∠DBE=90°.
此时,S=S△BDE=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 3 |
-
| ||||
| 6 |
当S=
| 1 |
| 3 |
-
| ||||
| 6 |
| ||
| 6 |
整理,得x2-2x+1=0.
解得x1=x2=1,即AD=1.
当90°<α<120°时,点D在AB的延长线线上(如图),

设AD=x,则BD=x-2,∠DBE=90°.
S=S△BDE=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 3 |
| ||||
| 6 |
当S═
| 1 |
| 3 |
| ||||
| 6 |
| ||
| 6 |
整理,得x2-2x-1=0.
解得 x1=1+
| 2 |
| 2 |
即AD=1+
| 2 |
综上所述:AD=1或AD=1+
| 2 |
点评:此题考查了相似形的综合,用到的知识点是平行线分线段成比例定理、相似三角形的判断与性质、旋转的性质以及三角形的面积公式等,关键是根据题意画出图形,注意分类讨论.

练习册系列答案
相关题目
若∠1=40.4°,∠2=40°4′,则∠1与∠2的关系是( )
| A、∠1=∠2 |
| B、∠1>∠2 |
| C、∠1<∠2 |
| D、以上都不对 |
正三角形的外接圆半径与内切圆的半径之比是( )
| A、1:2 | ||||
B、1:
| ||||
C、
| ||||
| D、2:1 |
若△ABC的外接圆的圆心在△ABC的内部,则△ABC是( )
| A、锐角三角形 | B、直角三角形 |
| C、钝角三角形 | D、无法确定 |
 把长方体的八个角切去一个角后,余下的图形有
把长方体的八个角切去一个角后,余下的图形有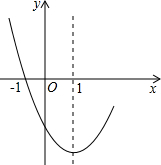 若二次函数y=x2-2x+c的部分图象如图所示,则关于x的方程x2-2x+c=0的两根为
若二次函数y=x2-2x+c的部分图象如图所示,则关于x的方程x2-2x+c=0的两根为