题目内容
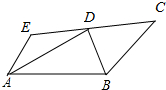 已知,如图,AE∥BC,AD、BD分别平分∠EAB、∠CBA,EC过点D.求证:AB=AE+BC.
已知,如图,AE∥BC,AD、BD分别平分∠EAB、∠CBA,EC过点D.求证:AB=AE+BC.考点:全等三角形的判定与性质
专题:证明题
分析:如图,作辅助线;首先证明AF⊥BD,进而证明△ABD≌△FBD,得到AB=BF;同理可证△ADE≌△FDC,得到CF=AE,问题即可解决.
解答: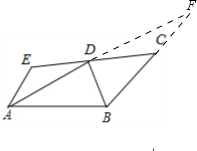 证明:如图,分别延长AD、BC交于点F;
证明:如图,分别延长AD、BC交于点F;
∵AD、BD分别平分∠EAB、∠CBA,
∴∠EAD=∠BAD=α,∠ABD=∠CBD=β;
∵AE∥BC,
∴2α+2β=180°,
∴α+β=90°,
即AF⊥BD;
在△ABD与△FBD中,
,
∴△ABD≌△FBD(ASA),
∴AB=BF,AD=DF;
同理可证:△ADE≌△FDC,
∴CF=AE,BF=BC+AE,
∴AB=AE+BC.
 证明:如图,分别延长AD、BC交于点F;
证明:如图,分别延长AD、BC交于点F;∵AD、BD分别平分∠EAB、∠CBA,
∴∠EAD=∠BAD=α,∠ABD=∠CBD=β;
∵AE∥BC,
∴2α+2β=180°,
∴α+β=90°,
即AF⊥BD;
在△ABD与△FBD中,
|
∴△ABD≌△FBD(ASA),
∴AB=BF,AD=DF;
同理可证:△ADE≌△FDC,
∴CF=AE,BF=BC+AE,
∴AB=AE+BC.
点评:该题主要考查了全等三角形的判定及其性质的应用问题;解题的关键是作辅助线,构造全等三角形;对综合的分析问题解决问题的能力提出了一定的要求.

练习册系列答案
相关题目
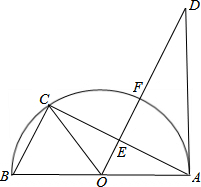 如图,AB是半圆O的直径,点C在半圆O上,过点O作OD∥BC交圆的切线AD于点D,交弦AC于E,交半圆于点F.
如图,AB是半圆O的直径,点C在半圆O上,过点O作OD∥BC交圆的切线AD于点D,交弦AC于E,交半圆于点F. 已知:AC和BD相交于点E,AB∥DC,AB=DC,试说明:BE=DE.
已知:AC和BD相交于点E,AB∥DC,AB=DC,试说明:BE=DE.
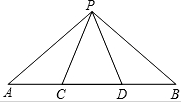 如图,在△PAB中,点C、D在AB上,PC=PD=CD,∠APB=120°,△APC与△BPD相似吗?为什么?
如图,在△PAB中,点C、D在AB上,PC=PD=CD,∠APB=120°,△APC与△BPD相似吗?为什么?