题目内容
7.(1)若$\sqrt{a+b+5}$+|2a-b+1|=0,则(b-a)2017=-1.(2)若单项式2x2ya+b与-$\frac{1}{3}$xa-by4是同类项,则a的值为3,b的值为1.
分析 (1)根据非负数的性质得出a、b的方程组,解之可得a、b的值,代入求值即可得;
(2)由同类项的定义得出关于a、b的方程组,解之可得.
解答 解:(1)根据题意,得:$\left\{\begin{array}{l}{a+b+5=0}\\{2a-b+1=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-2}\\{b=-3}\end{array}\right.$,
∴(b-a)2017=(-3+2)2017=(-1)2017=-1,
故答案为:-1;
(2)根据题意,得:$\left\{\begin{array}{l}{2=a-b}\\{a+b=4}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=3}\\{b=1}\end{array}\right.$,
故答案为:3,1.
点评 本题主要考查解二元一次方程组和非负数的性质、同类项的定义,根据题意得出方程组是解题的关键.

练习册系列答案
相关题目
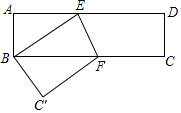 如图,将一张长方形纸片ABCD沿EF折叠,使点D与点B重合,点C落在C'的位置上.
如图,将一张长方形纸片ABCD沿EF折叠,使点D与点B重合,点C落在C'的位置上. 按如图样式在日历上用一个斜框框出三个数,若三个数和为51,则这三天中的第一天是这个月的9号.
按如图样式在日历上用一个斜框框出三个数,若三个数和为51,则这三天中的第一天是这个月的9号. 如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-1,1),B(-3,1),C(-1,4).
如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-1,1),B(-3,1),C(-1,4).